Podstawy matematyczne

Regina Tokarczyk

Na krakowskim Rynku - oprócz Sukiennic, pomnika Mickiewicza i Wieży Ratuszowej - znajduje się maleńki kościółek pod wezwaniem św. Wojciecha.

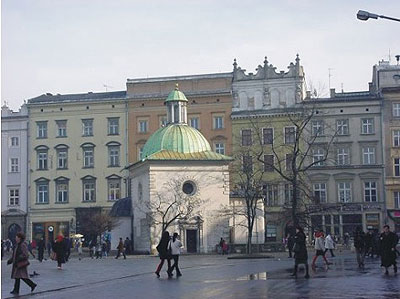
Rys. 1. Kościół pod wezwaniem św. Wojciecha w Krakowie

Oto wyniki nowoczesnej inwentaryzacji fotogrametrycznej tej XII-wiecznej budowli. Można je przedstawić w sposób tradycyjny (za pomocą rzutów, przekrojów, planów elewacji) albo też jako komputerowy trójwymiarowy model wektorowy (wire frame) lub model pokryty fikcyjnym materiałem z biblioteki oprogramowania.

Rys. 2. Kościół św. Wojciecha w Krakowie. Przekrój pionowy zewnętrza. W ramach pracy magisterskiej w ZFiIT wykonała Joanna Gacka.

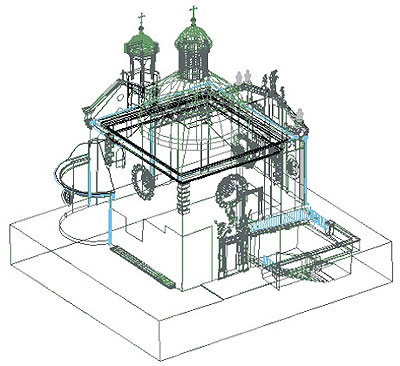
Rys. 3. Kościół św. Wojciecha w Krakowie. Model wektorowy 3D. W ramach pracy magisterskiej w ZFiIT wykonała Joanna Gacka.

Najlepiej zaś pokryć go fakturą odfotografowaną na zdjęciu, co przyda obrazowi realistycznego wyglądu. Taki sposób prezentacji zabytku umożliwia wirtualny spacer wokół niego, a jeśli inwentaryzacja jest całościowa - także obejrzenie wnętrza.

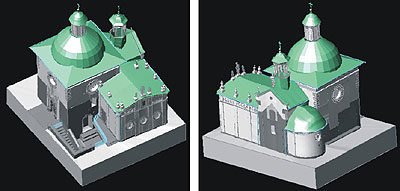
Rys. 4. Kościół św. Wojciecha w Krakowie. Zwizualizowany model powierzchniowy (AutoCAD). W ramach pracy magisterskiej w ZFiIT wykonała Joanna Gacka.

W jaki sposób można uzyskać przestrzenne współrzędne punktu w terenowym układzie odniesienia na podstawie zdjęcia fotogrametrycznego? Zgodnie z zasadą rzutowania, wektor promienia rzutującego w przestrzeni obrazowej kamery jest kolinearny (współliniowy) z wektorem w przestrzeni przedmiotowej. Współrzędne pierwszego wektora są wyznaczane przez elementy orientacji wewnętrznej kamery oraz położenie punktu obrazu w układzie tłowym, natomiast pozycję drugiego określa się w zewnętrznym układzie odniesienia (rys. 5). Kolinearność tę można zapisać w postaci prostej zależności:

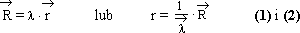
Sprowadzając obydwa wektory do tego samego układu, mamy:

(3) i (4)

gdzie:
- A jest ortogonalną macierzą transformacji przez kolejne obroty o kąty orientacji: ω, φ, κ przestrzennego układu tłowego zdjęcia w stosunku do układu odniesienia XYZ,
- X₀, Y₀, Z₀ to współrzędne środka rzutów w układzie odniesienia.
(Wielkości: X₀, Y₀, Z₀, ω, φ, κ nazywamy elementami orientacji zewnętrznej zdjęcia)

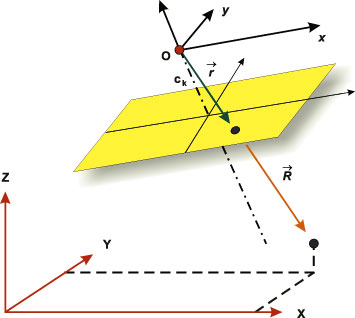
Rys. 5. Kolinearność wektorów w przestrzeni obrazowej i w przestrzeni przedmiotowej

Równanie kolinearności jest podstawą do rozwiązania większości problemów związanych ze znalezieniem przestrzennego położenia punktów. Pozwala ono również na wyznaczenie elementów orientacji zewnętrznej zdjęcia, co wymaga jednak znajomości współrzędnych tłowych i terenowych przynajmniej trzech punktów (tzw. fotopunktów).
Promień rzutujący odtworzony na podstawie zdjęcia fotogrametrycznego (rzutu środkowego) to zbyt mało, aby znaleźć położenie punktu w przestrzeni. Zależność (3) przy znanej orientacji zdjęcia daje tylko trzy równania z czterema niewiadomymi: X, Y, Z, λ. Dwa rzuty z dwóch różnych punktów umożliwiają natomiast wykonanie fotogrametrycznego wcięcia w przód (rys. 6), ponieważ kolinearność dwu promieni rzutujących daje 6 równań z pięcioma niewiadomymi: X, Y, Z punktu i współczynniki skali λ? i λ”.

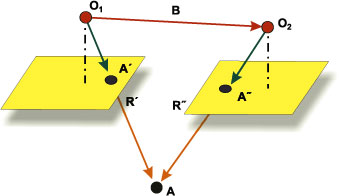
Rys. 6. Wyznaczenie położenia punktu na podstawie dwóch zdjęć

Z rys. 6 wynika, że wektor łączący oba środki rzutów (wektor bazy) oraz wektory rzutowe do punktu A są współpłaszczyznowe, czyli komplanarne. Warunek ten jest spełniony, gdy iloczyn mieszany tych wektorów jest równy zeru:

Warunek komplanarności wraz z warunkiem kolinearności jest stosowany przy wyznaczaniu przestrzennego położenia punktu, pozwala również na określenie wzajemnego położenia obu zdjęć w tzw. orientacji wzajemnej.
Fotogrametryczne pozycjonowanie wymaga zatem pomiaru na co najmniej dwóch zdjęciach odpowiadających sobie punktów - punktów homologicznych. Jeśli są to wyraźne i dobrze zdefiniowane szczegóły sytuacyjne, to pomiar ten nie nastręcza trudności. Ale co zrobić, jeżeli na przykład chcemy pomierzyć na zdjęciach lotniczych punkty, które mają posłużyć tylko jako pikiety wysokościowe, albo na zdjęciach naziemnych - odpowiadające sobie punkty na gładkiej powierzchni kopuły?
Z pomocą przychodzi wtedy sztuczny efekt stereoskopowy pozwalający na podstawie obserwacji dwóch (odpowiednio wykonanych) zdjęć uzyskać wrażenie przestrzenności obiektu. Jeżeli wykonamy zdjęcia tego samego obiektu z dwóch różnych miejsc w przestrzeni, osie zdjęć będą w przybliżeniu równolegle i prostopadłe do bazy. Uzyskany w ten sposób stereogram zdjęć normalnych po odpowiednim ułożeniu zdjęć pozwoli na uzyskanie efektu przestrzennego dla obszaru wspólnego dla obu zdjęć. Ale to nie wszystko. Wprowadzając do obserwowanego modelu przestrzenny znaczek pomiarowy (rys. 7), uzyskamy podwójną korzyść: możliwość pomiaru trudnych do identyfikacji punktów homologicznych i zrównanie dokładności pomiaru na zdjęciach poprzez ujednolicenie sygnalizacji punktów (sztucznym sygnałem - znaczkiem).

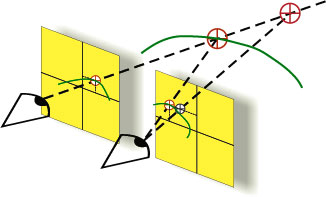
Rys. 7. Pomiar stereoskopowy za pomocą wirtualnego znaczka pomiarowego

Przyleganie znaczka do mierzonego punktu na modelu przestrzennym oznacza, że na obydwu zdjęciach zostaną znalezione i pomierzone odpowiadające sobie punkty. Takie pomiary umożliwiają wyznaczenie współrzędnych tłowych na zdjęciach, a potem przejście do interesujących nas wielkości w mierze terenowej. Minimalne przesunięcie jednego ze znaczków zgodnie z kierunkiem bazy będzie postrzegane jako jego przemieszczenie w kierunku "do" lub "od" obserwatora. Efekt głębi obiektu daje różnica paralaks podłużnych jego punktów, czyli różnic współrzędnych tłowych wzdłuż osi równoległej do bazy.
Znacząca większość opracowań fotogrametrycznych (zwłaszcza w zastosowaniach kartograficznych) wykorzystuje sztuczny efekt stereoskopowy. Stereogramy zdjęć normalnych ułatwiają również automatyzację pomiaru na zdjęciach, o czym mowa będzie dalej.

Dr hab. Regina Tokarczyk jest pracownikiem naukowym Zakładu Fotogrametrii i Informatyki Teledetekcyjnej Wydziału Geodezji Górniczej i Inżynierii Środowiska AGH w Krakowie