Niwelacja

Marcin Barlik, Magdalena Chruślińska

Opracowanie wyników obserwacji niwelacyjnych, poza poprawkami wynikającymi z czynności pomiarowych i z cech narzędzi (komparacyjna, termiczna), zawiera uwzględnienie poziomu odniesienia i systemu wysokości. Niniejszy artykuł zawiera uwagi o metodyce wprowadzanych grawimetrycznych poprawek do wysokości i przewyższeń w systemach występujących w Polsce na tle innych, stosowanych w Europie, systemów wysokości.


1. Wprowadzenie

Sieć wysokościowa w Polsce i innych krajach Europy Środkowej jest odniesiona do poziomu Morza Bałtyckiego w Zatoce Fińskiej, rejestrowanego na mareografie w miejscowości Kronsztadt pod St. Petersburgiem. Warto przypomnieć, że poziomy odniesienia sieci niwelacyjnych w różnych fragmentach naszego kontynentu różnią się między sobą i to o sporą ilość centymetrów. Poziom „zerowy” naszej sieci jest niższy o ok. 8 cm od obowiązującego na zachodzie Europy poziomu Morza Północnego w Amsterdamie. Przyczynami takiego stanu są przede wszystkim wpływy własności fizycznych mórz. Kwestia ta nie będzie jednak tutaj szerzej rozpatrywana.

Wprowadzenie systemu wysokości, czyli sposobu obliczania wzniesienia reperu nad poziomem morza, czy też przewyższeń między reperami jest niezbędne, bo obserwacje niwelacyjne wykonywane są w polu ziemskiej siły ciężkości. Powierzchnie równego potencjału tej siły, czyli powierzchnie poziome nie są do siebie równoległe na odcinku niwelacyjnym i dlatego zadaniem poprawki grawimetrycznej, jest uwzględnienie wpływu tej nierównoległości na wynik niwelacji. Definicja niwelacji precyzyjnej, oprócz wysokiej dokładności pomiaru, zawiera zatem konieczność wprowadzenia poprawek systemowych. Zwróćmy poza tym uwagę na fakt, że uzyskiwana wysokość w wyniku niwelacji geometrycznej (przy użyciu niwelatora, tachimetru, teodolitu) jest zupełnie innego rodzaju niż wysokość elipsoidalna (geodezyjna) wyznaczana z opracowania obserwacji satelitarnych w systemie GPS. Kwestię tę wyjaśniano w literaturze wielokrotnie, m in. w obszernej pozycji książkowej [Baran i inni, 1993].

Wpływ nierównoległości powierzchni równego potencjału na przewyższenie jest zależny od drogi niwelowania. Ponieważ przebieg powierzchni ekwipotencjalnej, prostopadłej w każdym punkcie do kierunku linii pionowej, jest ściśle związany z anomaliami grawimetrycznymi, dlatego do wyznaczenia systemowej poprawki niwelacyjnej niezbędne jest uzupełnienie pomiarów niwelacyjnych obserwacjami natężenia ziemskiego pola siły ciężkości. Należy przy tej okazji wyjaśnić, że zaniechanie obliczenia grawimetrycznych poprawek systemowych w opracowaniu pomiarów niższych klas niwelacji równoznaczne jest z powiększeniem błędów systematycznych i z interpoacją poprawki na odcinku między reperami wyższej klasy.

Przedkładane opracowanie zawiera uwagi o metodyce wprowadzanych grawimetrycznych poprawek do wysokości i przewyższeń w systemach występujących w Polsce na tle innych, stosowanych w Europie, systemów wysokości. W opracowaniu polskiej sieci niwelacji precyzyjnej zastosowano po 1956 r. system wysokości normalnych (Mołodienskiego). W odniesieniu więc do niego podane zostaną różnice wpływu modelowania przebiegu powierzchni poziomych. Eksperymenty dotyczyły terenu podgórskiego, w okolicach Grybowa pod N. Sączem, gdzie zainstalowano testowe pole geodezyjne Politechniki Warszawskiej i terenu nizinnego, na 30 km odcinku w południku Józefosławia pod Warszawą, gdzie znajduje się obserwatorium astronomiczno-geodezyjne Instytutu Geodezji Wyższej i Astronomii Geodezyjnej Politechniki Warszawskiej.


2. Istota zwykle stosowanych poprawek grawimetrycznych w systemach niwelacji

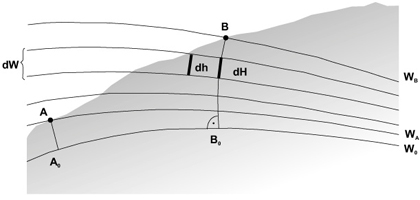
Rys. 1. Przekrój schematyczny przez ciąg niwelacyjny między punktami Ai B

Zacznijmy od ogólnego przypomnienia niezbędnych przesłanek teoretycznych z zakresu opracowania różnic wysokości. W niwelacji geometrycznej elementarne przewyższenie na stanowisku jest otrzymywane z różnicy odczytów na łatach przy poziomym położeniu osi celowej, czyli stycznie do powierzchni ekwipotencjalnej. Wyznaczenie przewyższenia między odległymi reperami polega na wielokrotnym powtórzeniu takiego elementarnego pomiaru różnic dh i ich zsumowaniu. W ciągu niwelacyjnym AB odstęp między sąsiednimi powierzchniami poziomymi dh jest różny od odstępu dH na linii pionu punktu końcowego tego odcinka. Wyjaśnia to rys. nr 1, na którym umieszczono pionowy przekrój przez kilka powierzchni ekwipotencjalnych. Przypomnijmy, że elementarny przyrost ziemskiego potencjału siły ciężkości dW między tymi powierzchniami przedstawia się wzorem:

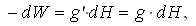
gdzie g’ i g są wartościami przyspieszenia siły ciężkości odpowiednio na ciągu niwelacyjnym i na linii pionu punktu B. Niezależną od drogi niwelowania jest różnica wartości potencjału siły ciężkości między punktami A i B, którą definiuje równość:

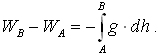
Zatem wielkością podstawową do zdefiniowania wysokości punktu A w dowolnym systemie wysokościowym jest różnica potencjału siły ciężkości w tym punkcie i potencjału na poziomie morza (geoidzie). Wyraża ona pracę, jaką należy wykonać przy przeniesieniu jednostkowej masy z powierzchni morza do punktu A na powierzchni Ziemi. Nazwana została ona wartością geopotencjalną i wyraża się wzorem:

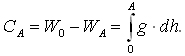
By wyrazić odstęp punktu A od poziomu morza w jednostkach długości, wartość geopotencjalną należy podzielić przez modelowe natężenie pola siły ciężkości, równe przyspieszeniu liniowemu w założonym modelu rozkładu siły ciążenia między powierzchnią Ziemi i powierzchnią odniesienia wysokości w definiowanym systemie.
Najprościej przedstawia się ten problem w systemie wysokości geopotencjalnych, gdyż dzielnikiem jest w nim wartość stała dla całej Ziemi, a mianowicie:
γ_k=10 ms^-2=100 Gal. Zatem wysokość geopotencjalna punktu A jest równa:

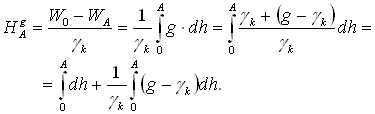
Przekształcenie doprowadziło do sumy dwóch całek, gdzie pierwsza to zaobserwowana różnica wysokości od poziomu morza do reperu A, druga oznacza grawimetryczną poprawkę geopotencjalną do wysokości zaobserwowanej niwelatorem. Równiełatwo jest okazać, że różnica wysokości geopotencjalnych między reperami A i B jest równa sumie przewyższeń i poprawki geopotencjalnej do przewyższenia, wykorzystującej natężenie siły ciężkości g_i na kolejnych odcinkach niwelacyjnych, czyli:

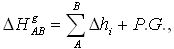
przy czym poprawka ta na odcinku AB wyraża się formułą:

W systemie wysokości geopotencjalnych Francuz Vignal i Duńczyk Simonsen wyrównali sieć niwelacji precyzyjnej w Europie zachodniej. W tym systemie wysokości punktów na tej samej powierzchni ekwipotencjalnej są jednakowe.
Podobną własność mają wysokości w systemie wysokości dynamicznych, zaproponowanym przez Voglera. Tym razem wzniesienie reperu nad geoidą wyraża wzór:

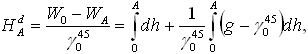
a różnica wysokości dynamicznych, wyrażona przez sumy, a nie całki wynosi:

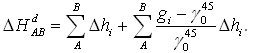
Wartością modelową przyspieszenia jest ciężkość na poziomie morza, na równoleżniku 45°, zdefiniowana przez Cassinisa tzw. wzorem międzynarodowym. Wynosi ona 980,6291 Gali. Ten system wysokości stosuje się w budownictwie wodnym. Powierzchnia wody w zamkniętym zbiorniku naturalnym ma bowiem taką samą wysokość dynamiczną. Poprawki dynamiczne do przewyższeń, jak się później okaże, mają mniejsze wartości niż poprawki geopotencjalne.
Przedstawiony teraz zostanie, w niezbędnym skrócie, system wysokości ortometrycznych, stosowany do 1956 r. na obszarze Polski. Wysokość ortometryczna reperu to jego odległość od geoidy, mierzona wzdłuż linii pionu w polu ziemskiej siły ciężkości. Ogólne wyrażenie na wysokość ortometryczną punktu A to:

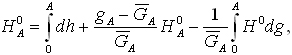
gdzie G_A oznacza przeciętne przyspieszenie na odcinku od geoidy do powierzchni Ziemi w pionie punktu A. Jest oczywiste, że wartości tej nie jesteśmy w stanie wyznaczyć ściśle, dlatego przy założeniu modelu rozkładu pola potencjalnego i gęstości w tej przestrzeni oblicza się przybliżenie wartości G_A. We wzorze na różnicę wysokości ortometrycznych, a mianowicie:

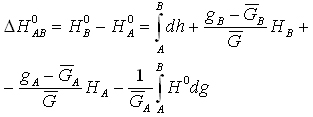
wartość pierwszej całki oznacza zaobserwowane przewyższenie między reperami, pozostałe są poprawką ortometryczną (P.O.) do różnicy wysokości. Metoda K. Niethammera wyznaczania poprawki ortometrycznej polega na realizacji wzoru:

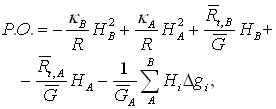
gdzie R to promień ziemski. Wymagane jest obliczenie następujących wyrażeń pomocniczych:

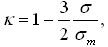
jako funkcji gęstości warstwy między geoidą i reperem s oraz gęstości średniej Ziemi s_m=5517 kg·m^-3 oraz poprawek terenowych przyspieszenia siły ciężkości, o czym nieco szerzej w dalszym tekście. Podamy, mianowicie, wzór na obliczenie przybliżonej, przeciętnej wartości przyspieszenia ziemskiego na odcinku od powierzchni Ziemi do poziomu morza, czyli:

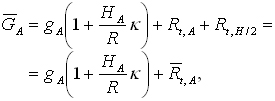
gdzie redukcja terenowa wartości g obliczona wokół stanowiska A wyraża się formułą:

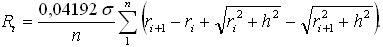
Nie omawiamy tu sposobu jej obliczania. W rezultacie wprowadzenia tego członu otrzymuj się siłę ciężkości odpowiadającą wygładzonej powierzchni terenu wokół A. Symbol h oznacza różnicę wysokości stanowiska i elementu rzeźby terenu, objętego promieniami strefy – wewnętrznym r_i i zewnętrznymr_i+1 oraz ramionami sektora wychodzącego ze stanowiska, stanowiącego 1/n kąta pełnego. Redukcja ta jest zawsze dodatnia. Natomiast redukcja topograficzna przeciętnej wartśi przyspieszenia, odtwarzająca grawitacyjny wpływ mas rzeźby terenu w punkcie zagłębionym na H/2 poniżej punktu A, ujęta jest wzorem:

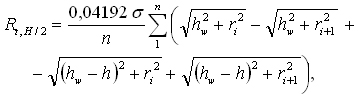
gdzie h_w oznacza głębokość poziomu odniesienia. Ta redukcja ma znak zależny od znaku przewyższenia h.
Suma redukcji topograficznych, występująca we wzorze na przeciętną ciężkość, może zostać pominięta w terenie o spokojnej rzeźbie. Tym samym otrzymuje się system wysokości ortometrycznych uproszczonych w myśl propozycji F. Helmerta. Niekiedy też, dla niedługiej (do ok. 40 km w warunkach polskich) linii niwelacyjnej zakłada się, że k_A=k_B=k. Wtedy poprawka ortometryczna do przewyższenia przyjmuje postać:

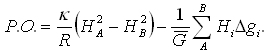
W omawianym systemie wysokości punktów na tej samej powierzchni ekwipotencjalnej są różne, bo różne są przeciętne wartości przyspieszenia na odcinkach od geoidy do tej powierzchni. Jeżeli zastosuje się w miejsce przeciętnych przyspieszeń rzeczywistych przeciętne przyspieszenia normalne, to stworzony zostanie tym samym system normalnych wysokości ortometrycznych. Był on stosowany w Polsce i innych, sąsiednich krajach przed II wojną światową.
W systemie wysokości normalnych, odpowiadającym teorii Mołodienskiego [Mołodienski i inni, 1960] badania kształtu Ziemi, powierzchnią odniesienia jest elipsoida ekwipotencjalna. Wysokości liczone są od tej powierzchni w normalnym polu siły ciężkości. Dlatego są one zdefiniowane wzorem:

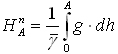
lub bardziej szczegółowym:

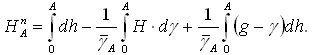
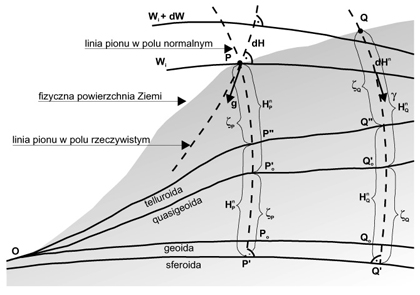
Rys. 2. Przedstawienie zależności przyrostu wysokości normalnej i przyspieszenia wzdłuż odcinka niwelacyjnego

Posługując się rys. 2 wyjaśniamy, że drugi człon poprawkowy do zaobserwowanej różnicy wysokości zawiera grawimetryczną anomalię wolnopowietrzną. Jest ona różnicą zaobserwowanej wartości przyspieszenia ziemskiego i wartości normalnej, obliczanej w myśl prawa rozkładu ciężkości w polu elipsoidy poziomowej. W Polsce, jak na razie, stosuje się wzór podany przez Helmerta na początku wieku z uzupełniającym członem, wynikającym z poprawy dokonanej w 1971 roku, po korekcie przyspieszenia wyjściowego w Poczdamie. Na elipsoidzie w funkcji szerokości geograficznej wyraża się przez równanie:

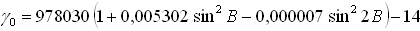
podające wartość w miliGalach (10^-5 m·s^-2). Na powierzchni Ziemi, gdzie oblicza się anomalie, wartość przyspieszenia wynosi:

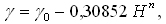
natomiast przeciętne na linii normalnego pionu punktu A, między elipsoidą ekwipotencjalną i tzw. telluroidą określane jest w myśl wzoru:

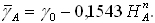
Różnica wysokości normalnych powstaje w myśl formuły:

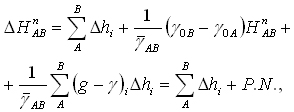
gdzie dzielnikiem jest średnia z przeciętnych wartości przyspieszenia normalnego na odcinku między reperami A i B. Z wystarczającą dokładnością może być obliczana dla średniej szerokości geograficznej i średniej wysokości obu punktów.
Na podstawie przedstawionych powyżej wzorów można dojść do formuł transformujących wysokości w różnych systemach. Punktem wyjścia jest porównanie wartości geopotencjalnych w tych systemach. Dla przykładu, z wysokości normalnej otrzymuje się wysokość geopotencjalną w myśl równania:

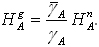
Trzeba jednak pamiętać, że wysokości w tych dwóch systemach są odniesione do dwóch różnych powierzchni normalna do quasigeoidy Mołodienskiego, geopotencjalna, podobnie jak ortometryczna i dynamiczna, do geoidy.

3. Inne systemy wysokości poddane analizie

Poza przedstawionymi w rozdz. 2 systemami wysokości geometrycznych spotyka się w pomiarach specjalnych, w budownictwie tunelowym i drogowym jeszcze inne, wymienione poniżej.
J. Vignal w 1952 r. opracował system wysokości sferoidalnych zmodyfikowanych. Mianownik podstawowej formuły na wysokość w tym systemie ma postać:

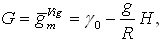
a więc zawiera zarówno przyspieszenie zaobserwowane na reperze, jak i ciężkość normalną.
G. Bomford [Bomford, 1984] zaproponował stosowanie systemu wysokości quasi-dynamicznych, gdzie modelowa ciężkość przeciętna wyznaczana jest ze wzoru:

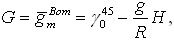
a jej stosowanie zmniejsza wartości poprawek w stosunku do systemu wysokości dynamicznych.
W badaniach dotyczących określania pionowego gradientu siły ciężkości na podstawie anomalii grawimetrycznych V. Baranov zastosował system wysokości pseudosferycznych. Ciężkość modelowa określana jest w nim w myśl formuły:

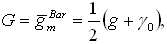
a więc jako średnia z wartości ciężkości zaobserwowanej na powierzchni Ziemi i normalnej na elipsoidzie. Jest to zatem system bardzo uproszczony, wysokości systemowe są wyraźnie związane z rzeźbą terenu.
Prof. K. Ledersteger, zauważywszy spore wartości poprawek dynamicznych, opracował system wysokości dynamicznych – zredukowanych. Definiuje się je poprzez zastosowanie wartości geopotencjalnej i członu poprawkowego, a mianowicie:

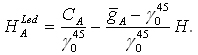
Wartości poprawek są zależne od rozbieżności przeciętnego przyspieszenia w pionie reperu i ciężkości normalnej na równoleżniku 45°.
W opracowaniu lokalnych pomiarów niwelacyjnych, dla celów budowlanych, K. Ledersteger również zalecał stosowanie zmodyfikowanych wysokości sferycznych. Ciężkość modelowa, czyli mianownik we wzorze na wysokość, zdefiniowany jest jak następuje:

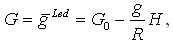
przy czym G₀ oznacza średnią na obszarze prac (nie większym niż 20·20 km) wartość przyspieszenia zredukowanego wolnopowietrznie g₀. Prowadzi to do zminimalizowania grawimetrycznych poprawek niwelacyjnych. Przypomnijmy, że redukcja wolnopowietrzna przyspieszenia to dodanie do zaobserwowanej ciężkości wpływu jej gradientu pionowego i wzniesienia nad powierzchnią odniesienia. Wyraża tę operację formuła:

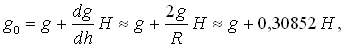
gdzie wysokość należy wprowadzać w metrach a wynik otrzymany zostanie w mGal.
Z innych systemów, stosowanych w obsłudze budownictwa, przedstawimy propozycję K. Ramsayera. Poprawka do przewyższenia w tym wypadku ma postać:

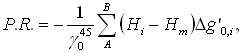
przy czym H_i to średnia wysokość odcinka a H_m oznacza średnią wysokość terenu na placu budowy lub wysokość poziomu odniesienia prac niwelacyjnych a Dg’_0,i to różnica ciężkości z wprowadzoną redukcją Bouguera na odcinku niwelacyjnym. Ten system wysokości, bardzo „technicznych”, ma poprawki mniejsze niż w systemie Helmerta i dla wysokości dynamicznych. Redukcja Bouguera przyspieszenia siły ciężkości interpretowana jest jako usunięcie grawitacyjnego wpływu masy płyty zawartej między poziomem stanowiska i powierzchnią odniesienia. Wartość ciężkości po wprowadzeniu tej redukcji to:

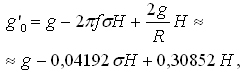
gdzie f oznacza współczynnik grawitacji.
Inne, rzadziej stosowane systemy wysokości, wprowadzali do prac pomiarowych i badań naukowych m. in. Salboni, Colomba-Pres, Baeschlin [Böhm i inni, 1981]. Ten ostatni zalecał zastosowanie redukcji izostatycznej dla uzyskania modelowego przyspieszenia w myśl teorii Pratta – Hayforda, z głębokością kompensacji 80 km. A. Berroth zaproponował użycie poziomej powierzchni odniesienia leżącej zewnątrz Ziemi.
Przeliczanie wysokości wyrażonych w ostatnio omówionych systemach następuje, tak jak poprzednio podano, przez porównanie wartości geopotencjalnych. W wyniku prostych przekształceń możliwe jest wyznaczenie, na przykład, wysokości normalnych na podstawie wysokości quasi-dynamicznych. W tym wypadku bowiem:

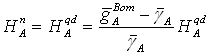
4. Analiza porównawcza przedstawionych systemów wysokości

W tym rozdziale podamy wyniki wyznaczeń grawimetrycznych poprawek niwelacyjnych na dwóch obiektach. Pierwszy z nich to ciąg niwelacyjny w terenie podgórskim, w okolicach Grybowa. Ma długość 36630 m. Zawiera 12 reperów – znaków uniwersalnych, na których możliwe jest również wykonanie pomiarów techniką satelitarną GPS [Rogowski i inni, 1997]. W tablicy 1 umieszczono informacje niwelacyjne i grawimetryczne, niezbędne do obliczenia wartości geopotencjalnych i poprawek systemowych.

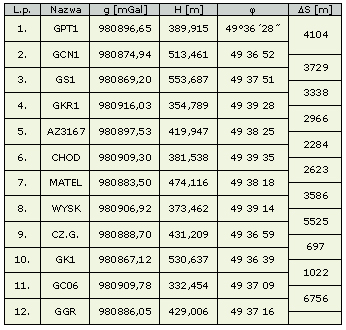
Tablica 1. Zestawienie informacji do określenia grawimetrycznych poprawek w systemach wysokości geometrycznych w okolicach Grybowa

Natomiast w tablicy 2 podano wartości (w metrach) niwelacyjnych poprawek geopotencjalnych, poprawek dynamicznych, ortometrycznych (Helmerta) i normalnych. Z zestawienia tego wynika, że największe wartości przyjmują w terenie podgórskim poprawki geopotencjalne. Sięgają kilku metrów dla przewyższeń stumetrowych. Mniejsze, bo kilkucentymetrowe są poprawki dynamiczne. Ciekawe jest, że poprawki w systemie wysokości normalnych różnią się generalnie znakiem od poprawek w systemie Helmerta. Zastosowano przy tym gęstość utworów podpowierzchniowych na tym obszarze s = 2,145 g·cm^-3 określoną na podstawie zdjęcia grawimetrycznego. Poprawki ortometryczne (P.O.) są większe bezwzględnie od poprawek normalnych (P.N.). Chociaż w tablicy podano korekcje systemowe do przewyższeń, to łatwo zauważyć, że wysokości nad poziomem morza są zdecydowanie różne w systemie geopotencjalnym (P.G.) i dynamicznym (P.D.) od innych systemów. Wysokości ortometryczne i normalne różnią się na tym terenie od siebie o kilka centymetrów.

Tablica 2. Poprawki do różnic wysokości w terenie podgórskim w okolicy Grybowa pod Nowym Sączem w ośmiu analizowanych systemach niwelacyjnych

W tablicy tej umieszczono także wyniki wyznaczeń poprawek niwelacyjnych w systemach wysokości: zmodyfikowanych sferoidalnych (P.M.), quasi-dynamicznych (P.K.), pseudosferycznych (P.P.) i dynamicznych zredukowanych (P.L.). Do wyznaczenia wyrażeń poprawkowych ( n. p. promień wodzący powierzchni ekwipotencjalnych) zastosowano parametry elipsoidy Krasowskiego. Najłatwiej oblicza się poprawki pseudosferyczne. Zauważamy, że poprawki do przewyższeń w systemie wysokości quasi-dynamicznych są niewiele mniejsze od poprawek geopotencjalnych. Poprawki do różnic wysokości sferoidalnych zmodyfikowanych i pseudosferycznych są wyraźnie mniejsze. Prawie dwa razy mniejsze są od nich poprawki w systemie wysokości dynamicznych zredukowanych. Ujemne na całym ciągu są poprawki geopotencjalne, normalne i quasi-dynamiczne. Dodatnie okazują się poprawki w pozostałych pięciu analizowanych systemach.
Podsumowując ten punkt naszych rozważań stwierdzamy, że nie jest obojętne w terenie podgórskim a tym bardziej górzystym, w którym systemie liczy się różnice wysokości. Rozbieżności bowiem przewyższeń w różnych systemach są wielokrotnie większe od dozwolonych błędów pomiarów w niwelacji geometrycznej, nie tylko precyzyjnej.

Drugim obiektem, na którym wyznaczono systemowe poprawki niwelacyjne, to grawimetryczna baza południkowa, w terenie nizinnym, pod Warszawą. Rozciąga się od Warszawy (Politechnika) w kierunku na południe do wsi Jaroszowa Wola, na długości ok. 28 km [Barlik i inni, 1980]. Stanowiska na profilu służą do okresowych wyznaczeń grawimetrycznych i satelitarnych w celu monitorowania zmian kierunku pionu w obserwatorium. Przewyższenia na tym ciągu nie przekraczają 15 m. Punktem środkowym jest stanowisko permanentnych obserwacji satelitarnych techniką GPS w ramach działalności Międzynarodowej Służby Geodynamicznej GPS [Śledziński, 1998]. W tablicy 3 podano informacje niezbędne do dalszych obliczeń.

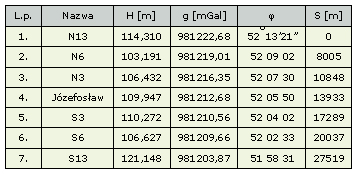
Tablica 3. Zestawienie informacji do określenia grawimetrycznych poprawek w systemach niwelacyjnych na nizinnym profilu w południku Józefosławia pod Warszawą

W tablicy 4 zamieszczono wartości poprawek niwelacyjnych w przedstawionych ośmiu systemach, tych samych co i zastosowanych w okolicach Grybowa. Gęstości objętościowe utworów podpowierzchniowych niezbędne do obliczeń poprawek ortometrycznych zaczerpnięto z map gęstości dla obszaru Polski [Fajklewicz i inni, 1965]. Na profilu zawierały się w granicach od 2,04 w okolicach Warszawy do 2,02 g·cm^-3 we wsi Jaroszowa Wola. Poprawki wyrażone są w metrach.

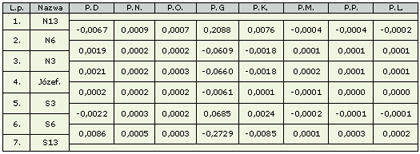
Tablica 4. Grawimetryczne poprawki systemowe do różnic wysokości na południkowym profilu w okolicach Warszawy

Analizując ostatnie zestawienie stwierdzamy, że największe są i na nizinach poprawki geopotencjalne do różnic wysokości. O wiele mniejsze są poprawki normalne i ortometryczne. Mają nawet porównywalne ze sobą wartości. Bezwzględne wartości poprawek dynamicznych i quasi-dynamicznych są bardzo zbliżone. Można zauważyć, że poprawki do przewyższeń sferoidalnych zmodyfikowanych, pseudosferycznych i zredukowanych dynamicznych są w tej okolicy przy mniej precyzyjnych pracach zaniedbywalne. Natomiast różnice wysokości wyrażone w różnych systemach są ze sobą nie porównywalne nawet w terenie równinnym.


5. Podsumowanie

Opracowanie nasze miało na celu zwrócenie uwagi na konieczność konsekwentnego stosowania systemu wysokości w pracach niwelacyjnych, czyli wykorzystania modelowego rozkładu przyspieszenia siły ciężkości a co za tym idzie i geometrii powierzchni ekwipotencjalnych w skorupie Ziemi. Wpływ pola ciężkościowego na wyniki niwelacji, jak wykazano, jest bezsporny. Przedstawiona analiza porównawcza kilku systemów wysokości geometrycznych udowodniła, że występujące na terenie Polski anomalie przyspieszenia są na tyle znaczące, że ich zaniedbanie spowoduje duże błędy w wynikach niwelacji. Jest oczywiste, że bliskie powiązanie polskiej sieci wysokościowej z sieciami europejskimi spowoduje konieczność ujednolicenia systemu.
Analizując poprawki do różnic wysokości stwierdzamy, że ich wartości są bardzo zależne od pofałdowania terenu i wzniesienia ciągu nad poziomem odniesienia. Poprawki do pomiarów w terenie górzystym są znacznie większe od poprawek w terenie nizinnym. Rodzaj systemu niwelacyjnego rzutuje także na wartości poprawek. Najmniejsze poprawki uzyskuje się w systemach wysokości ortometrycznych i normalnych (Mołodienskiego). Zwróćmy uwagę także na fakt, że różnice wysokości opracowane w różnych systemach w terenie równinnym są do siebie bardzo zbliżone. Czasem więc nie ma znaczenia, który system wysokościowy tam wprowadzimy.
Podkreślmy na zakończenie, że zasadniczą wielkością, wyjściową w każdym systemie jest wartość geopotencjalna występująca na znaku wysokościowym. To ona powinna znaleźć się w banku danych niwelacyjnych. Wtórna jest wysokość obliczona w przyjętym systemie niwelacji geometrycznej.

Literatura

• Baran L. W., i inni, (praca zbiorowa), 1993. Niwelacja precyzyjna – niwelacja geometryczna, trygonometryczna, satelitarna i hydroniwelacja. Polskie Przedsiębiorstwo Wydawnictw Kartograficznych im. E. Romera S.A., Warszawa.
• Barlik M., Galas R., Rogowski J., 1980. Variations of the geographical latitude at Józefosław Observatory and their comparison with gravimetrical determinations. Prace Naukowe Politechniki Warszawskiej, s. Geodezja, z. 23. Warszawa.
• Bomford G., 1984. Geodesy. Oxford, at the Clarendon Press.
• Böhm J, Hora L., Kolenaty E., 1981. Vyąąi geodézie, Dil.2. Ceske Vysoke Uceni Technicke, Praha.
• Fajklewicz Z., Rejman T., 1965. Mapy ciężarów objętościowych skał. Technika Poszukiwań, Nr 14. Wyd. Geolog., Warszawa.
• Mołodienski M.S., Jeremiejev I.F. Jurkina M.I., 1960. Mietody izuczenija vnieszniego gravitacjonnogo polja Ziemli. Trudy CNIIGAiK, Vyp. 131, Moskva.
• Niethammer T., 1932. Nivellement und Schwere als Mittel zur Berechnung wahrer Meereshöhen. Veröff. Schweiz. Geod. Komm., Heft 32, Basel.
• Rogowski J., Barlik M., Kujawa L., Margañski S., Pachuta A., Piraszewski M., Walo J., Hefty J., Husar L., 1997. Determination of geoidal heights in the test field at Grybów – status report ’95. Reports on Geodesy, No. (2)25, Warsaw University of Technology, Institute of Geodesy and Geodetic Astronomy, Warsaw.
• Śledziński J., 1998. Permanent GPS stations in CEI countries and their contribution to the international programmes. Reports on Geodesy. No. 10(40), Warsaw University of Technology, Institute of Geodesy and Geodetic Astronomy, Warsaw.

(Opracowanie umieszczono na GeoForum w maju 2007 r.)