|
Wykorzystanie pionowego gradientu ziemskiej siły ciężkości w niektórych zagadnieniach geodezyjnych
Marcin Barlik
W poniższych rozważaniach przedstawiono w skrócie możliwość zastosowania zaobserwowanych szybkości pionowych zmian ciężkości ziemskiej do rozwiązywania problemów związanych z opracowaniem elementów geodezyjnych.
Oczywiste jest, że przez pionowy gradient przyspieszenia rozumie się ubytek natężenia pola ciężkości przy wzniesieniu się o 1 m nad powierzchnię Ziemi. Wykorzystanie wartości pionowego gradientu ciężkości ziemskiej G jest szerzej znane w geofizyce poszukiwawczej, w rozpoznawaniu płytkich struktur anomalnych pod względem gęstości, zalegających w skorupie Ziemi. W geodezji fizycznej zaobserwowana szybkość zmian przyspieszenia ziemskiego w kierunku pionowym służy do rozwiązania zadania redukcji obserwacji na powierzchnię odniesienia, do wyznaczania systemowych poprawek niwelacyjnych (Barlik i inni, 1999) i konstrukcji warunku granicznego geodezji fizycznej w celu określenia odstępu geoidy od elipsoidy ziemskiej.
Obecnie do pomiaru gradientu wykorzystuje się precyzyjne grawimetry, których dokładność nominalna pomiaru różnicy przyspieszenia zbliża się do mikrogala (1 mGal = 10-8 m/s-2). Stosując zatem instrumenty LaCoste & Romberg i Scintrex Autograv CG-3, można określać G z błędem nie większym od 10 Etweszy (1 E = 10-9/s-2). Ponadto skonstruowano precyzyjne gradientometry pionowe zarówno statyczne, jak i dynamiczne – satelitarne i lotnicze.
Wartość pionowego gradientu przyspieszenia siły ciężkości wyznaczona zostaje przez pomiar składowych wchodzących do ilorazu różnicy przyspieszenia Dg na pionowym odcinku Dh, zwykle o długości ok. 1 m, czyli
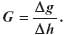
Zdawać sobie należy sprawę, że wartość ta może znacznie odbiegać od normalnej G, obliczonej w myśl formuły właściwej dla stosowanej powierzchni odniesienia prac grawimetrycznych – odpowiedniej elipsoidy ziemskiej (Barlik, 1991). Na obszarze Polski wartość G (w systemie globalnym GRS ’80) mieści się w granicach od -3,0854 do -3,0847 mm/s-2/m-1. Dla ogólnej orientacji podajmy, że w okolicach Grybowa, gdzie znajduje się geodezyjne pole testowe Politechniki Warszawskiej, na stanowiskach wyznaczeń gradientometrycznych wartość G zawarta jest w granicach od -4,048 do -2,212 mm/ s-2/ m-1, czyli od -4048 do -2212 Etweszy. Pod Warszawą, na terenie Obserwatorium Astronomiczno-Geodezyjnego Instytutu Geodezji Wyższej i Astronomii Geodezyjnej PW, wartości gradientu pionowego mieszczą się w przedziale od -2719 do -3181 Etweszy. Zatem anomalie pionowego gradientu DG, czyli różnice wartości pomierzonej i normalnej, znacznie przewyższają błąd określenia tej wielkości. Jak można się zorientować, stosowanie wartości normalnej G zamiast rzeczywistej w zagadnieniach objętych tematem niniejszej rozprawy wprowadza spore błędy do określanych elementów geodezyjnych.
Pionowy gradient przyspieszenia ziemskiego w opracowaniu pomiarów przyciągania
Grawimetry do obserwacji absolutnych i względnych skonstruowane są w taki sposób, że ich system pomiarowy (wyrzutnia ciężaru w aparacie balistycznym lub układ sprężyn w grawimetrze statycznym) definiuje rezultat pomiaru na pewnej wysokości nad znakiem grawimetrycznym. W przypadku aparatu balistycznego miejsce to, czyli wierzchołek toru, może osiągać wysokość nawet 1 m. Czujnik grawimetru statycznego przy pomiarach sieci podstawowych i wzorcowych, jak Unification of Gravity Systems in Central and Eastern Europe (UNIGRACE) w Europie Środkowej odnosi wartość ciężkości na wysokości ok. 25 cm nad stanowiskiem. W grawimetrycznych pomiarach poszukiwawczych, czy przy zaopatrywaniu reperów niwelacyjnych w poprawki grawimetryczne, jest to znacznie więcej.
W wypadku redukcji grawimetrycznych pomiarów bezwzględnych aparatami balistycznymi (a takich stanowisk jest na terenie Polski kilkanaście) stosuje się procedurę określania g w myśl równania kwadratowego, czyli:
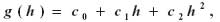
a zatem gradient pionowy przyspieszenia określony zostaje w myśl formuły:
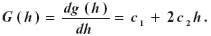
Zgodnie z zaleceniami międzynarodowymi (Robertsson i inni, 1998) pomiary wartości gradientu wykonuje się grawimetrem statycznym nad stanowiskiem aparatu balistycznego na trzech wysokościach, a to 0,05, 0,9 i 1,3 m. Standard taki obowiązuje także na stacjach międzynarodowej sieci podstawowych stanowisk wyznaczeń absolutnych – International Absolute Gravity Basestation Network (IAGBN), gdzie monitoruje się wartość przyspieszenia metodą balistyczną. Kampaniom komparacyjnym grawimetrów absolutnych, organizowanym średnio co cztery lata w Międzynarodowym Biurze Miar i Wag w Sévres pod Paryżem, towarzyszą precyzyjne wyznaczenia wartości G. Wykazały one, że wartość gradientu nad sześcioma słupami w laboratorium Biura wahała się w granicach od -3020 do -2483 Etweszy na wysokości 0,9 m, a na wysokości 1,3 m – w granicach od -2456 do -2951 Etweszy. O tym, że sprawa jest niebagatelna, przekonują nas wartości redukcji rezultatów pomiarów do punktów odniesienia ze względu na występowanie zmian przyspieszenia wraz ze zmianą wysokości. W kampanii z 1997 r. osiągały one wartości od -158 mGal do +122 mGal w zależności od typu i egzemplarza instrumentu. W Sévres umowna redukcja przyspieszenia następowała do wzniesienia 0,9 m nad górną powierzchnią słupa. Polski absolutny aparat balistyczny, skonstruowany w Politechnice Warszawskiej przez Zbigniewa Ząbka (Ząbek, 1994, 1996), podaje wartość przyspieszenia na wysokości ok. 0,354 m nad poziomem znaku grawimetrycznego.
Przeprowadzone przy współudziale autora eksperymenty (Pachuta i inni, 1998) na północnej części krajowej bazy grawimetrycznej (od Warszawy po Elbląg), wykazały, że wartości gradientu pionowego zawierały się w granicach od -0,2970 do -0,3115 mGal/m. Poprawki różnic przyspieszenia na przęsłach bazowych ze względu na wzniesienie systemu mierzącego wynikające z rozbieżności normalnego i zaobserwowanego gradientu osiągały wartości od -5,2 do +7,7 mGal. Tym samym, kalibracja grawimetrów, czyli uzyskanie współczynników k1 i k2 przeliczenia odczytów grawimetru n na wartość tzw. referencyjnej ciężkości w myśl równania skali instrumentu:
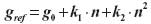
lub prościej, w przypadku liniowej skali, do wyznaczenia przyrostu przyspieszenia:
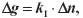
doprowadzić może do błędów względnych większych niż 10-4 / k, uznawanych przez przepisy pomiarowe G 1.2. „Pomiary grawimetryczne i ich opracowanie” za błąd dopuszczalny.
Zespół z Politechniki Warszawskiej opracował odpowiednie procedury postępowania i specjalistyczny program GRAWGRAD na komputer polowy Psion Organiser LZ64 w celu zautomatyzowania grawimetrycznych pomiarów kalibracyjnych wykonywanych różnymi instrumentami z niezbędnym uwzględnieniem anomalii pionowego gradientu przyspieszenia. Redukcję do znaku pomiarowego wykonuje się przez wprowadzenie zaobserwowanej wartości gradientu, czyli
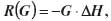
przy czym DH oznacza wzniesienie (obniżenie) systemu mierzącego grawimetru statycznego nad (pod) znakiem pomiarowym (marką na słupie, reperem itd.).
Pionowy gradient przyspieszenia w systemach niwelacji
O problemie wprowadzania systemowych poprawek grawimetrycznych do wyników niwelacji geometrycznej była już w GEODECIE mowa (Barlik i inni, 1999). Przypomnijmy w tym miejscu, że pionowy gradient przyspieszenia tzw. wolnopowietrzny, czyli wyznaczony nad powierzchnią Ziemi bez uwzględnienia mas topograficznych, jest niezbędny do określenia przeciętnej wartości przyspieszenia na drodze od geoidy do reperu. W obliczeniach następuje redukcja przyspieszenia do połowy wysokości punktu nad poziomem odniesienia (np. poziomem morza). Do dalszej analizy wybierzmy, z wielu omówionych poprzednio, niwelacyjną poprawkę ortometryczną. Do jej określenia niezbędne staje się wyznaczenie gradientu pionowego przyspieszenia w polu siły ciężkości, niestety, często zastępowanego wartością gradientu normalnego. Powołamy się dalej na analizę zagadnienia określenia dokładności anomalii grawimetrycznych w opracowaniu wyników niwelacji precyzyjnej (Bokun, 1958). W pozycji tej wykazano, że dla uzyskania błędu średniego poprawki niwelacyjnej nie większego od 0,1 mm, przy przewyższeniu w granicach do 80 m między reperami, niezbędne jest określenie anomalii grawimetrycznej z błędem nie większym od 1,1 mGal = 1,1•10-5• m• s-2. Anomalia wolnopowietrzna to:
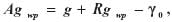
gdzie pomierzoną wartość przyspieszenia g uzupełnia się redukcją grawimetryczną wolnopowietrzną Rgwp i zestawia z wartością normalną przyspieszenia ziemskiego γ0, określaną wzorem wynikającym z teorii pola normalnego siły ciężkości (Barlik, 1991). Więcej wiadomości związanych z tym problemem Czytelnik znajdzie również w podręczniku Kazimierza Czarneckiego (Czarnecki, 1997). Interesujący nas gradient pionowy ciężkości występuje w redukcji na drodze Hred od punktu grawimetrycznego do poziomu odniesienia (np. geoidy), gdyż
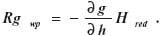
Przypisując temu składnikowi dopuszczalny błąd 0,1 mGal, wnoszony do błędu anomalii, określimy dopuszczalny błąd gradientu w wypadku redukcji grawimetrycznej przy wyznaczaniu systemowej poprawki niwelacyjnej, a mianowicie:
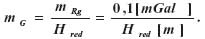
Błędność gradientu to, oprócz błędów pomiaru tego parametru, przede wszystkim jego anomalia DG. Łatwo dowieść, że dla wysokości redukcji 100 m, dopuszczalny błąd anomalii DG może wynieść 10 Etweszy. W terenie podgórskim punkt o wysokości 500 m wymaga znajomości gradientu pionowego z błędem nie większym niż 2 Etwesze, by błąd poprawki systemowej nie przekroczył 0,1 mm. Zdajemy sobie w tej chwili sprawę, że do wystarczająco dokładnego określenia poprawek niwelacyjnych ze względu na istnienie pola siły ciężkości wymagany jest bezpośredni pomiar pionowego gradientu przyspieszenia ziemskiej siły ciężkości, a nie zastosowanie jego wartości normalnej. W systemie wysokości normalnych (Barlik i inni, 1999) taka operacja jest zbędna, gdyż określenie poprawki normalnej opiera się na przyjęciu normalnego, sferoidalnego rozkładu pola siły ciężkości między elipsoidą poziomową a powierzchnią Ziemi.
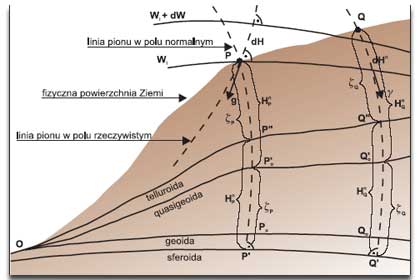
Rys. 1. Przedstawienie zależności przyrostu wysokości normalnej i przyspieszenia wzdłuż odcinka niwelacyjnego
Pionowy gradient przyspieszenia w wyznaczeniu rozbieżności w przebiegu geoidy względem quasi-geoidy
Z poruszoną w poprzednim rozdziale kwestią uzupełnienia wyników prac niwelacyjnych wartościami pionowego gradientu przyspieszenia ziemskiego wiąże się ściśle kwestia rozróżnienia położenia powierzchni odniesienia w systemach wysokości – ortometrycznych i normalnych. Wywody teoretyczne prowadzące do wyznaczenia różnicy odstępu geoidy od elipsoidy ziemskiej N i wzniesienia quasi-geoidy Mołodienskiego z nad elipsoidą (inaczej anomalii wysokości) znaleźć można w literaturze (Sjöberg, 1995), (Barlik, 1997a i 2000a). Nie wnikając zatem w kolejne etapy wyprowadzenia wzorów, zauważamy, że rozpatrywana różnica jest równa różnicy wysokości reperu w systemie ortometrycznym i w systemie normalnym (pomijając odchylenia pionu), a zatem jest funkcją przeciętnych wartości przyspieszenia ziemskiego w polu rzeczywistym i w polu normalnym na drogach od powierzchni odniesienia do powierzchni Ziemi, czyli:
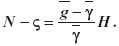
Wstawienie do tego wzoru odpowiednich formuł na wartości przeciętne prowadzi, po kilku przekształceniach, do wyraźnego związku z pionowym gradientem przyspieszenia w miejscu określania odległości geoidy od quasi-geoidy, a mianowicie:
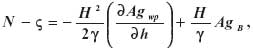
gdzie drugi składnik wyraża wpływ anomalii grawimetrycznej Bouguera. Anomalia ta zdefiniowana jest przez równanie:
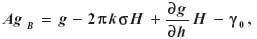
gdzie k oznacza stałą grawitacji Newtona, s to gęstość utworów podpowierzchniowych i występuje również pionowy gradient przyspieszenia siły ciężkości. Skupmy uwagę na pierwszym składniku prawej strony omawianej różnicy wzniesień geoidy i quasi-geoidy. Mieszczący się tam pionowy gradient anomalii wolnopowietrznej można przedstawić następująco:
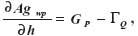
a więc jako anomalię pionowego gradientu. Gradient pionowy siły ciężkości GP określany jest na stanowisku na powierzchni Ziemi, normalny GQ – w punkcie Q leżącym na wysokości normalnej nad elipsoidą poziomową. Nie jest on identyczny z punktem P , bo wysokość normalną odkładamy od elipsoidy, nie od geoidy, i po normalnej, a nie rzeczywistej linii pionu. Powołując się na rys. 1 (opublikowany w pozycji Barlik i inni, 1999), powiemy, że punkt P dzieli od punktu Q anomalia wysokości, czyli odstęp telluroidy od powierzchni Ziemi.
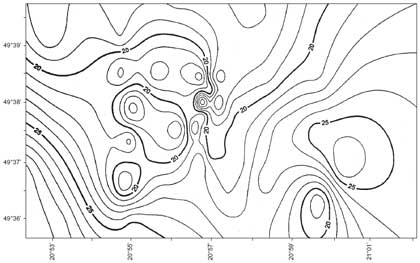
Rys. 2 Izolinie wpływu anomalii gradientu pionowego na odstęp geoidy i quasi-geoidy w okolicach Grybowa (podane w milimetrach)
Ilustracją wywodów jest rys. 2, na którym przedstawiono izolinie wpływu anomalii gradientu pionowego na odstęp N - z w okolicach Grybowa pod Nowym Sączem, gdzie zlokalizowane jest geodezyjne pole testowe Politechniki Warszawskiej. Punkt PW10 leży w bezpośrednim sąsiedztwie Ośrodka Szkoleniowego PW. W tym podgórskim terenie wysokości n.p.m. zawierają się w granicach od ok. 300 m do ok. 700 m. Zauważmy, że wkład anomalii gradientu sięga 15 mm, zatem jest nie do pominięcia w czasie badania tzw. geoidy sub-centymetrowej. Pod Warszawą wkład anomalii gradientu pionowego do wzniesienia geoidy nad quasi-geoidę jest o wiele mniejszy, bo sięga zaledwie 0,25 mm.
Wymaganą dokładność określania pionowego gradientu przyspieszenia określa się przez zastosowanie prawa przenoszenia się błędów średnich. Stąd otrzymamy:
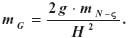
Można dociec, że dla założenia błędu różnicy odstępów nie większego niż 1 mm i wzniesienia stanowiska nad powierzchnią odniesienia – 100 m, błąd określenia pionowego gradientu nie powinien przekraczać 1960 Etweszy. Dla wysokości 500 m błąd dopuszczalny maleje do ok. 80 Etweszy. Są to wartości łatwe do uzyskania nowoczesnym sprzętem grawimetrycznym.
Określanie kształtu geoidy z anomalii pionowego gradientu przyspieszenia siły ciężkości
Anomalie pionowego gradientu przyspieszenia ziemskiego mogą służyć do określenia odstępów geoidy od elipsoidy dwojako. Podobnie jak ma to miejsce w przypadku anomalii grawimetrycznych, w teorii Stokesa badania figury Ziemi, i tutaj stosuje się rozwiązanie równania różniczkowego drugiego stopnia, w którym argumentem jest anomalia gradientu DG. Problem ten był przedmiotem wcześniejszego opracowania autora (Barlik, 1997a). Druga droga to wprowadzenie odpowiednich poprawek do odstępów geoidy wyznaczonych na drodze niwelacji geodezyjnej ze względu na anomalie pionowego gradientu, co bardziej detalizuje undulacje, uwzględniając zakłócenia pochodzące od utworów podpowierzchniowych. I ta kwestia była przedmiotem prac autora (Barlik, 2000b).
Nie wnikając zbytnio w szczegóły wyprowadzeń odpowiednich wzorów, podamy formułę, która służy do określenia odstępu geoidy przez anomalie pionowego gradientu przyspieszenia, a mianowicie:
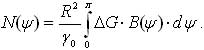
Występująca tu funkcja wagowa odległości sferycznej B(y) od stanowiska może być łatwo realizowana przy obliczeniach. Jest ona bowiem malejąca z odległością, bo:
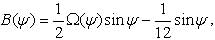
a funkcja W(y), analogon funkcji Stokesa przy wyznaczeniach z anomaliami grawimetrycznymi, ma postać:
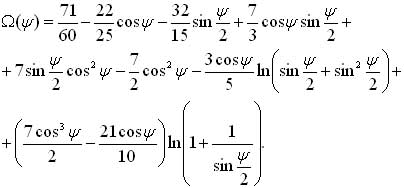
Postępowanie praktyczne polega zatem na podziale pola anomalii gradientu na strefy, w zależności od odległości sferycznej, dalej na wyznaczeniu średnich anomalii w strefach i numerycznej realizacji całki na odstęp geoidy.
Interesująca jest analiza wymagań co do dokładności określenia wartości pionowego gradientu G, by uzyskać odstęp geoidy N z założonym błędem. Zależność między błędami potencjału zakłócającego dT, który jest odpowiedzialny za odstęp, i błędami gradientu pionowego d(DG) jest następująca:
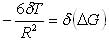
Przyrost potencjału zależny jest od odstępu geoidy w myśl zależności Brunsa, zmodyfikowanej do postaci:
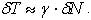
Zakładając wartość błędu odstępu geoidy dN=1 cm, otrzymuje się dopuszczalny błąd gradientu wynoszący d(DG) = 1,45/10-5 E, czyli błąd względny tej charakterystyki – 5/10-9. Jest to bardzo wysokie wymaganie co do dokładności wykonywanych naziemnych pomiarów gradientometrycznych. Obniżając wymagania, zauważamy, że do otrzymania błędu odstępu nie większego niż 1 m, należy anomalię gradientu wyznaczyć z błędem nie przekraczającym 0,00145 E. Odpowiada to błędowi względnemu 4,7/10-7 określenia G oraz takiemu samemu błędowi wyznaczenia różnicy przyspieszenia ziemskiego przy pomiarze na odcinku pionowym o długości 1 m. Taką dokładność jesteśmy w stanie współcześnie osiągnąć, bo wartość d(Dg) = 4,7 mGal nie jest wygórowana.
Rachunek tu podany jest bardzo zgrubny, bo sprowadził się do wprowadzenia tylko jednego stanowiska. Szersza analiza wykazuje, że anomalie gradientu należy określić w najbliższym otoczeniu stanowiska (do ok. 11 km) z błędem nie większym niż 20 Etweszy, by określić odstęp w wyniku całkowania z błędem 1 cm.
Gradientometryczne poprawki w niwelacji wysokości geoidy
Zasadę stosowania gradientometrycznego wyrazu korekcyjnego do wyników niwelacji astronomiczno-geodezyjnej wyjaśnimy, stosując procedury analogiczne do wykorzystywanych w wyznaczeniach odstępów geoidy przy użyciu anomalii grawimetrycznych. Wyjściowe jest równanie określające różnicę tych odstępów przez odchylenia pionu:
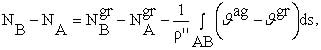
przy czym zarówno dla odchyleń astronomiczno-geodezyjnych, jak i grawimetrycznych jest:
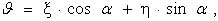
jako funkcja azymutu a boku AB. Człony Ngr wyznaczane są przez całkowanie anomalii.
W przypadku stosowania niwelacji do odległości nie większej niż 30 km, jak ma to miejsce w naszej krajowej sieci POLREF, można bez zmniejszenia dokładności zastąpić całkę sumą, a różnica odstępów geoidy wyrazi się wzorem:
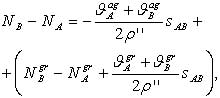
gdzie w pierwszym składniku znalazły się składowe astronomiczno-geodezyjnych odchyleń pionu.
Postępując podobnie jak w rozważaniach związanych z wyznaczeniem tej poprawki przez całkowanie anomalii przyspieszenia, można przyjąć, że jej obliczenie nastąpi przez całkowanie anomalii gradientu pionowego w skończonym obszarze S, w którym znajduje się całkowicie zanurzony odcinek AB = 2l, a promień całkowania w takim kołowym obszarze wokół każdego ze stanowisk jest jednakowy i równy iloczynowi promienia Ziemi R i ustalonej odległości sferycznej y0, czyli r = Ry0. Autor udowodnił (Barlik, 2000b), że wpływ pozostałego pola S' nieuwzględnionych anomalii pionowego gradientu przyspieszenia ziemskiego może być oszacowany, jeśli poznamy przeciętną wartość tych anomalii w odległości r. Odpowiednia formuła ma bowiem postać:
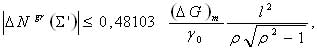
przy czym r = RS/l jest ilorazem promienia całkowania i połowy odległości między stacjami A i B. Do otrzymania wpływu anomalii gradientu mniejszego od 1 cm w terenie podgórskim wystarcza zastosować zasięg całkowania do r = 1,8. Zatem przy realizacji wzoru na różnicę odstępów geoidy zastosować można w obliczeniu pierwszego komponentu wyprowadzony poprzednio wzór roboczy (Barlik, 2000b):
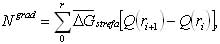
używając przeciętnych wartości anomalii w kolejnych strefach między promieniami ri i ri+1, na które podzielono pole anomalii gradientu. Funkcja tu wprowadzona to:
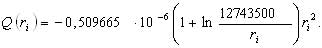
Dla ogólnej orientacji podajmy, że w okolicach Grybowa wartości tego składnika przy sumowaniu wpływu gradientu do 4500 km sięgały 23 mm.
Określenie wartości drugiego członu poprawki gradientometrycznej polega na uwzględnieniu tego samego fragmentu pola anomalii gradientu pionowego, jak przy wyznaczeniach Ngrad. Postulat taki wynika z teorii niwelacji odstępów geoidy (Pellinen i inni, 1982). Przywołamy teraz odpowiedni wzór na składową w południku stanowiska, a mianowicie:
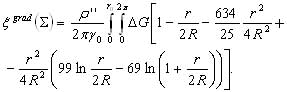
Po przeprowadzeniu analizy wartości granic wyrażeń w otoczeniu punktu do r0,
dochodzi się do uproszczonych – w celu dalszych oszacowań – formuł na składową południkową (Barlik, 2000c). Na rysunku 3 przedstawiono izolinie wartości poprawek do wysokości geoidy, obliczonych z całkowania pola anomalii pionowego gradientu. Poprawki te dotyczą wysokości uzyskanych z niwelacji astronomiczno-geodezyjnej w okolicach Grybowa. Ilustracja obejmuje centralny fragment pola testowego przedstawionego na rysunku 2. Poprawki odniesione są one do stanowiska PW10, który jest punktem sieci europejskiej EUREF i polskiej osnowy podstawowej POLREF, był stanowiskiem kampanii satelitarnej WEDOC i wielu innych. Zauważamy, że wartości tych poprawek zawierają się w granicach od –15 do +15 mm, na dość przecież stosunkowo niewielkim obszarze, bo ok. 20 km2.
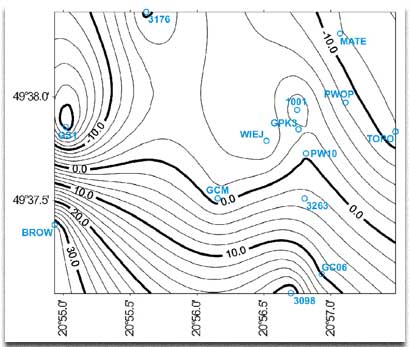
Rys. 3. Poprawki gradientometryczne w niwelacji wysokości geoidy w okolicach Grybowa w odniesieniu do punktu PW10 (Grybów) sieci EUREF (podane w milimetrach)
W celu wyznaczenia poprawek gradientometrycznych, pole całkowania DG dzieli się na szereg stref i sektorów, a w tak powstałych segmentach uśrednia się wartości anomalii pionowego gradientu ciężkości. Błąd średni w odchyleniu pionu, wnoszony przez błędy gradientu dG w strefie o numerze m, oszacowuje się na podstawie równania:
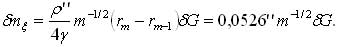
W zależności zatem od zasięgu sumowania można obliczyć dopuszczalne błędy określenia wartości pionowego gradientu. Odwołując się do okolic Grybowa, podamy, że dla uzyskania błędu poprawki nie większego niż 1 mm w najbliższym otoczeniu stanowiska do 1 km, wymagany jest błąd określenia anomalii gradientu nie większy niż 0,0027 mGal/m = 27 Etweszy. Od tej odległości do 4,5 km należy wyznaczyć DG z błędem nie przewyższającym 11 Etweszy, a dalej od punktu niwelacji geoidy dopuszczalny błąd średni nie powinien być większy niż 18 Etweszy. Taką dokładność można obecnie uzyskać poprzez pomiar grawimetrem statycznym na pionowym jednometrowym odcinku.
Pionowy gradient przyspieszenia siły ciężkości w redukcjach obserwacji geodezyjnych na powierzchnię odniesienia
Poruszona w tytule tego rozdziału kwestia jest związana z wyznaczeniem kątowego wpływu krzywizny linii pionu na odcinku od fizycznej powierzchni Ziemi do poziomu morza. Odsyłając Czytelnika do literatury (Ząbek, 1964), podamy poniżej, że wpływ taki w płaszczyźnie południka miejsca obserwacji wyraża się wzorem:
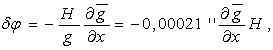
natomiast w płaszczyźnie pierwszego wertykału:
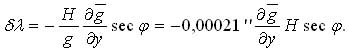
Występujące w obydwu wzorach występują składowe poziomego gradientu przeciętnego przyspieszenia (odpowiednio w południku i w pierwszym wertykale stanowiska i wyrażone) powinny zostać w mGal/km, a wysokości stanowisk w metrach. Jednak do określenia wartości przeciętnej przyspieszenia ziemskiego na linii pionu stanowiska od powierzchni Ziemi do poziomu odniesienia użyć musimy gradientu pionowego, bowiem w myśl koncepcji Poincarégo i Preya jest:
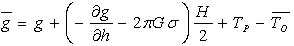
przy czym TP jest poprawką topograficzną przyspieszenia w punkcie na powierzchni Ziemi, a T0 – w punkcie na połowie wysokości stanowiska nad poziomem odniesienia. Pierwsza z tych poprawek interpretowana jest jako matematyczne wygładzenie terenu wokół stanowiska, druga polega na odtworzeniu grawitacji wygładzonych mas w punkcie na połowie wysokości stanowiska geodezyjnego nad powierzchnią odniesienia.
Na marginesie głównego nurtu naszych rozważań podajmy, że redukcja kierunku poziomego na elipsoidę odniesienia (następnie odwzorowywanego na płaszczyznę), spowodowana występowaniem krzywizny linii pionu, jest zdefiniowana wzorem:
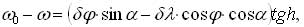
gdzie h jest kątem podniesienia (pionowym) kierunku, a jego azymutem oraz j szerokością geograficzną stanowiska. Redukcjom takiego rodzaju muszą również zostać poddawane obserwacje z zakresu geodezyjnych pomiarów inżynierskich (Brovar, 1983).
I jeszcze jedna uwaga. Dotyczy ona redukcji sieci satelitarnej na geoidę. Jeśli chcemy wykorzystać tę sieć do unowocześnienia istniejącej osnowy, to zmuszeni jesteśmy do stosowania takich samych metod redukcji współrzędnych na geoidę. W procesie redukcji sieć satelitarna nie może doznać zniekształceń w stosunku do sieci określonej innymi metodami geodezyjnymi. Kwestię tę naświetlił Kazimierz Czarnecki (Czarnecki, 1980). Zauważył mianowicie, że współrzędne stanowisk satelitarnych należy tak zredukować, by odpowiadały kierunkowi cięciwy linii pionu między powierzchnią Ziemi i geoidą. Stąd też odpowiednie korekcje:
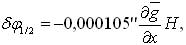
dla szerokości geograficznej i dla długości
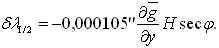
Dla uproszczonej analizy ustalmy, że do określenia gradientu poziomego zmian przeciętnego przyspieszenia używamy odcinka Dx o rozpiętości 1 km w południku i Dy na wschód od stanowiska. Ponadto zaniedbać można różnicę poprawek topograficznych, co odpowiada zastosowaniu systemu ortometrycznych wysokości w myśl koncepcji Helmerta (Barlik i inni, 1999). Łatwo wtedy wykazać, że dopuszczalny błąd wyznaczenia wartości pionowego gradientu siły ciężkości wyniesie:
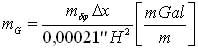
i odpowiednio dla mdl.
Jeśli redukcja współrzędnych ma zostać określona z błędem nie większym niż 0,001˝, to dla wysokości stanowiska nad poziomem redukcji H = 100 m otrzymuje się dopuszczalny błąd wyznaczenia gradientu równy 50 Etweszy. W okolicach Grybowa dopuszczalny błąd mG nie może przekroczyć (dla powyższych założeń co do dokładności redukcji) wartości 2 Etweszy. Jest oczywiste, że nie można w żadnym razie zastosować w tym procesie gradientów przyspieszenia normalnego, gdyż anomalie tej charakterystyki nawet na nizinach wyraźnie przekraczają wyżej określone dopuszczalne błędy.
Podsumowanie
Sumując powyższe rozważania, można wyrazić pogląd, że dostępny współcześnie sprzęt grawimetryczny pozwala na uzyskanie wartości pionowego gradientu przyspieszenia siły ciężkości wytwarzanej przez Ziemię z dokładnością wystarczającą do celów badawczych i praktycznych. W treści artykułu wykazano możliwość zastosowania anomalii tej charakterystyki do określenia kształtu Ziemi, podobnie jak anomalii grawimetrycznych. Wskazano na możliwości poprawienia, w celu lepszej detalizacji, wyników niwelacji wysokości geoidy i wyznaczenia odchyleń pionu. Przedstawione zobrazowania służą za dowód ważności wpływu anomalii pionowego gradientu na położenie geoidy.
Celem podjętego tematu było też wskazanie konieczności uzupełniania obserwacji geodezyjnych, przed ich dalszym odwzorowaniem, poprawkami wynikającymi z anomalii, rzeczywistego pionowego gradientu przyspieszenia ziemskiej siły ciężkości. Tego wymaga współcześnie uzyskiwana precyzja wyznaczeń elementów osnów geodezyjnych i współrzędnych stanowisk.
Profesor Marcin Barlik był pracownikiem Instytutu Geodezji Wyższej i Astronomii Geodezyjnej Politechniki Warszawskiej
Literatura
- Barlik M., 1991, Normalna ciężkość dla obszaru Polski w globalnych systemach odniesienia. „Przegląd Geodezyjny” nr 9, Rok LXIII, Wyd. Sigma, Warszawa.
- Barlik M., 1997a. Wykorzystanie anomalii pionowego gradientu siły ciężkości w badaniu figury Ziemi. „Zeszyty Naukowe Akademii Rolniczej we Wrocławiu”, s. Geodezja i Urządzenia Rolne, t. XIV, nr 324, Wrocław.
- Barlik M., 1997b. On the application of gradientometric measurements in determining the separation between the geoid and Molodensky's quasigeoid. „Reports on Geodesy”, No. 2 (25), Warsaw University of Technology, Warsaw.
- Barlik M., Chruślińska M., 1999. O systemach niwelacji geometrycznej. GEODETA nr 4 (47), Warszawa.
- Barlik M., 2000a, On the contribution of the vertical gravity gradient anomalies to the separation between the geoid and Molodensky’s quasigeoid (basing on the example of the geodetic test field near Grybów). „Reports on Geodesy” No. 2 (50), Warsaw University of Technology, Warsaw.
- Barlik M., 2000b, Gradientometric corrections to the geoidal heights levelling. „Reports on Geodesy” No. 2 (50), Warsaw University of Technology, Warsaw.
- Barlik M., 2000c. On the determination of plumb-line deflections using vertical gravity gradient anomalies in the geodetic test field near Grybów. „Reports on Geodesy” No. 2 (50), Warsaw University of Technology, Warsaw.
- Bokun J., 1958, Przygotowanie i opracowanie materiałów grawimetrycznych dla potrzeb polskiej sieci astronomiczno-geodezyjnej i sieci niwelacji precyzyjnej I klasy. „Prace IGiK” Nr 1 (13), t. VI, Warszawa.
- Brovar V.V., 1980, Gravitacjonnoje pole v zadaczach inżeniernoj geodezii. Izdat. „Niedra”, Moskva.
- Czarnecki K., 1980, Teoria satelitarnego orientowania i skalowania podstawowych poziomych sieci geodezyjnych. Wydawn. Politechniki Warszawskiej, „Prace Naukowe Geodezja”, z. 22, Warszawa.
- Czarnecki K., 1997. Geodezja współczesna w zarysie. Wyd. Wiedza i Życie, Warszawa.
- Pachuta A., Barlik M., Kalinowska-Śledzińska B., Margański S., Walo J., 1998, Poprawka w sieciach grawimetrycznych uwzględniająca rzeczywisty pionowy gradient siły ciężkości, VI Sympozjum Komitetu Geodezji PAN „Współczesne Problemy Podstawowych Sieci Geodezyjnych”, Warszawa, 3-4 września, 1998.
- Pellinen L.P., Deumlich F., 1982, „Theoretische Geodäsie” VEB Verlag für Bauwesen, Berlin.
- Robertsson I. oraz 35 współautorów, 1999 Results from the Fifth International Comparison of Absolute Gravimeters, ICAG'97, „Metrologia” No. 43, Paris.
- Sjöberg L.E., 1995. On the geoid to quasigeoid separation, „Manuscripta Geodaetica”, Vol. 20, No.8.
- Ząbek Z., 1964. Redukcje obserwacji astronomicznych na geoidę i obserwacji geodezyjnych na elipsoidę odniesienia. „Zeszyty Naukowe Politechniki Warszawskiej” nr 84, „Geodezja” nr 12, Politechnika Warszawska, Warszawa.
- Ząbek Z., 1994. The ballistic gravimeter of the Institute of Geodesy and Geodetical Astronomy WUT, „Reports on Geodesy” No. 1(9), Warsaw University of Technology, Warsaw.
- Ząbek Z., 1996. The transportable ballistic gravimeter ZZG. „Reports on Geodesy” No. 3(21), Warsaw University of Technology, Warsaw.
(Opracowanie umieszczono na Geoforum w marcu 2007 r.)
|
