|
Wprowadzenie do grawimetrii geodezyjnej, cz. II
Marcin Barlik
Przyjrzyjmy się teraz technologii pomiarów przyspieszenia ziemskiego metodami balistycznymi i statycznymi. Pierwsze precyzyjne pomiary balistycznymi grawimetrami absolutnymi datuje się od lat 60. XX w. Stosuje się od tego czasu w grawimetrii aparaty wykorzystujące rzut pionowy ciała w próżni.
Zasada pomiarów grawimetrami balistycznymi
Poniżej nieco uwag z teorii ruchu ciała (próbnika) w próżniowym cylindrze aparatu balistycznego. Jak wiadomo z kursu mechaniki, ruch jednostajnie przyspieszony pod działaniem stałego przyspieszenia siły ciężkości g0 ujęty jest równaniem różniczkowym drugiego stopnia o postaci:
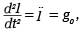
gdzie ï oznacza drugą pochodną drogi względem czasu. Oś odległości skierowana jest pionowo ku dołowi. Dwukrotne całkowanie tej funkcji prowadzi do wzoru:
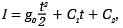
przy czym stałe C1 i C2 można uzyskać po uwzględnieniu warunków początkowych rozwiązania poprzedniego równania. W momencie rozpoczęcia zliczania czasu przebiegu (czyli t = 0) prędkość ciała wynosi v0 = v(0), a odległość od początku układu w tym momencie l(0) = l0. Zatem równanie ruchu przyjmuje postać:
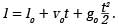
Ruch ciała obserwuje się na odcinku o długości do 1 m, a wymagany współcześnie względny błąd średni wyznaczenia przyspieszenia to 10-9. Dlatego należy koniecznie uwzględniać zmiany przyspieszenia ziemskiego wzdłuż całej trajektorii. Wartość g0 odnosi się do początku lokalnego układu współrzędnych. Biorąc pod uwagę niejednorodność pola siły ciężkości, równanie ruchu będzie następujące:
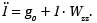
Korzystając z teorii rozwiązań równań różniczkowych, otrzymuje się na koniec wyrażenie na przyspieszenie w początku układu współrzędnych, a mianowicie:
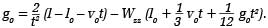
Ostatni człon prawej strony tego równania traktuje się jako poprawkę ze względu na istnienie pionowego gradientu przyspieszenia siły ciężkości na stanowisku obserwacyjnym. Poprawka ta ma wartość równą ok. 0,8 mm/s-2. Gradient Wzz wyznacza się za pomocą grawimetru statycznego. Przy określaniu g0 niezbędna jest rejestracja momentu przejścia ciała w co najmniej trzech punktach, czyli pomiar dwóch odcinków drogi i dwóch interwałów czasu.
Rozróżnia się symetryczne i niesymetryczne sposoby rejestracji. Symetryczny sposób polega na obserwacji ruchu ciała najpierw pionowo w górę, a następnie, po osiągnięciu górnego wierzchołka toru, spadającego swobodnie. Pomiar drogi i czasu wykonywany jest na symetrycznych względem wierzchołka częściach trajektorii. Niesymetryczny pomiar absolutnej wartości przyspieszenia to obserwacje jedynie swobodnego spadku ciała w rurze próżniowej. Z niezbędną dokładnością mierzy się odległości między poziomami rejestracji przy użyciu interferometru laserowego Michelsona.
Do pomiarów balistycznych sposobem niesymetrycznym służył aparat skonstruowany przez J.E. Fallera i J.A. Hammonda z University Vesli, Princeton, USA. Pomiar pojedynczy rejestrował długości drogi pryzmatu na odcinku ok. 1 m. Aparat ten zbudowany został w latach 1968-69, uznawany jest obecnie za instrument pierwszej generacji.
W 1981 r. w Joint Institute for Laboratory Astrophysics (JILA), National Bureau of Standards and University of Colorado (USA) wykonano pierwsze pomiary aparatem Fallera, który jest aparatem tzw. trzeciej generacji. Przy jego konstrukcji wykorzystano zasadę swobodnego spadku pryzmatu. Źródło światła stanowi w tym instrumencie laser stabilizowany zaprojektowany przez Zeemana. Kontrola częstotliwości zapewniona jest w instrumencie JILA przez rubidowy atomowy zegar. Grawimetr ten odróżnia się od wcześniejszych konstrukcji nowym urządzeniem próbnika opuszczanego w rurze próżniowej oraz inną izolacją od długookresowych wibracji podstawy i gruntu. Ciało spadające, w kształcie czworościanu z kryształu, umieszczone jest w pojemniku próżniowym, który również opada w aluminiowej rurze zewnętrznej. Droga próbnika wynosi ok. 20 cm. Ma on tę właściwość, że odbija promień padający na podstawę ściśle równolegle. W przypadku obrotu pryzmatu wokół dowolnej osi, przechodzącej przez punkt wewnątrz bryły, zwany środkiem optycznym, nie pojawia się różnica dróg optycznych, czyli tzw. chód optyczny przyrządu. Od 1987 r. kolejne udoskonalone mutacje tego grawimetru nazywane były JILA-g z odpowiednim numerem.
Dr J.E. Faller skonstruował grawimetr balistyczny, niesymetryczny, z supersprężyną kompensującą mikrosejsmy, zwany od jego nazwiska FG, który był produkowany od początku lat 90. w wersji FG-5 przez firmę AXIS Instruments Company. Miał masę ok. 320 kg oraz objętość sześciu kontenerów z aparaturą ok. 1,5 m3. Pod koniec lat 90. firma amerykańsko-kanadyjska MICRO-g SOLUTIONS Inc. rozpoczęła produkcję małego grawimetru absolutnego FG5-L z konstrukcją podobną do uproszczonego rozwiązania zastosowanego w FG-5. Ma on masę tylko ok. 60 kg. Rura próżniowa ze statywem ma wysokość ok. 70 cm. Z serii pomiarów trwającej 10 minut otrzymuje się absolutne przyspieszenie ziemskie z błędem do 0,5 µm/s-2. Powtarzalność wyników na stanowisku szacowana jest na 0,1 µm/s-2. Produkowane są także aparaty typu A-10 o zbliżonych parametrach, dostosowane do pomiarów na punktach terenowych, nie tylko w laboratoriach. Ta sama firma przejęła też od AXIS produkcję grawimetrów FG-5. Tego typu instrument o numerze fabrycznym 230 kupiła w 2005 r. Politechnika Warszawska. Został on zainstalowany w Obserwatorium Astronomiczno-Geodezyjnym w Józefosławiu pod Warszawą.

Autor podczas uruchamiania grawimetru FG-5 w obserwatorium PW w Józefosławiu pod Warszawą
(fot. P. Jakubicka)
Przy symetrycznym sposobie obserwacji przyspieszenia ziemskiego w aparacie balistycznym rejestruje się interwały T i t między momentami przejścia wyrzucanego pionowo ciała odpowiednio przez pary: dolna i górna stacja, na częściach trajektorii symetrycznych względem jej wierzchołka. Odstęp H między poziomami rejestracji jest ściśle wyznaczony interferencyjnie. Na poziomie dolnej stacji zachodzi równość:
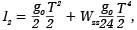
a z kolei na górnej:
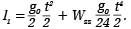
Stąd oczywiście wynika, że przyspieszenie ziemskie wynosi:
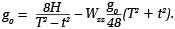
Wzór powyższy jest ideową formułą. Na jej podstawie pracuje od połowy lat 60. zeszłego stulecia aparat balistyczny skonstruowany w Sévres pod Paryżem przez fizyka japońskiego A. Sakumę z grupą geofizyków francuskich. Na bazie koncepcji przyrządu A. Sakumy dwie instytucje – Bureau International de Poids et Measures w Sévres oraz Instituto di Metrologia (IMGC) „G. Colonnetti” w Turynie – zbudowały wspólnie przewoźny grawimetr absolutny. W 1977 r. przystąpiono przy jego użyciu do pomiarów na punktach podstawowej osnowy grawimetrycznej w zachodniej Europie. Skala długości w tym instrumencie jest określana na podstawie długości fali helowo-neonowego lasera kontrolowanej z błędem rzędu 5/10-9. Licznik prążków interferencyjnych i dwa liczniki sygnałów czasu emitowanych przez rubidowy wzorzec mają stabilność 10-10 na 10 dób. Ruch próbnika odbywa się w próżni o ciśnieniu 0,1 hPa. Masa całego grawimetru wynosi ok. 600 kg. Instrumentem tym wykonano również pomiary na 17 stacjach europejskiej bazy grawimetrycznej – od Hammerfestu w Norwegii do Katanii na Sycylii i dalej aż do Nairobi. Na każdym stanowisku obserwacje trwały 3-4 dni, obejmując od 40 do 140 wyznaczeń. Błąd średni średniej wartości przyspieszenia wahał się w granicach od 0,02 do 0,04 mm/s-2.
Począwszy od 1980 r. opisany powyżej typ absolutnego grawimetru, po kilku udoskonaleniach, zaczęto produkować seryjnie we Francji w firmie Jaeger oraz we Włoszech z oznaczeniem A-60. Tym grawimetrem wykonano pomiary również w Polsce, m.in. w Obserwatorium Astronomiczno-Geodezyjnym Politechniki Warszawskiej w Józefosławiu pod Warszawą i w Lamkówku, w Obserwatorium Satelitarnym Akademii Rolniczo-Technicznej w Olsztynie (obecnie Uniwersytet Warmińsko-Mazurski).
Dodajmy w tym miejscu, że przewaga metody symetrycznego pomiaru nad obserwacjami niesymetrycznymi wiąże się przede wszystkim z możliwością eliminacji minimalnego wpływu tarcia cząstek pozostałego powietrza podczas ruchu próbnika w górę i w dół, które oddziałuje z różnym znakiem. Wyższa jest także dokładność pomiaru interwałów czasu między przejściami przez poziomy rejestracji.

Grawimetr absolutny prof. Zbigniewa Ząbka
(fot. archiwum Instytutu Geodezji Wyższej i Astronomii Politechniki Warszawskiej)
Oryginalną konstrukcję posiada grawimetr balistyczny zbudowany przez prof. Zbigniewa Ząbka w Instytucie Geodezji Wyższej i Astronomii Geodezyjnej Politechniki Warszawskiej [Ząbek, 1996]. Ruch symetryczny masy próbnej na odległości ok. 20 cm obserwowany jest w tym aparacie na kilkuset poziomach (od 300 do 3000). W kloszu grawimetru utrzymywane jest ciśnienie ok. 0,1 Pa. Całkowita masa aparatu wynosi ok. 120 kg. Trójścienny reflektor, o wadze ok. 80 g, wykonany z płaskich sklejonych luster, katapultowany jest za pomocą urządzenia o podobnej konstrukcji jak w grawimetrze Sakumy. Układ mierzący drogę reflektora ruchomego stanowią oprócz niego: reflektor w sejsmografie, fotodiody i laser helowo-neonowy stabilizowany z dokładnością 10-9 w okresie miesiąca. Jest on porównywany ze stacjonarnym laserem jodowym AXIS/BIPM ISL 1 o stabilności 10-10 w dwuletnim interwale czasu. Wzorzec czasu stanowi oscylator kwarcowy Rohde-Schwarz XSD 2 o stabilności częstotliwości 10-9 w okresie miesiąca. Impulsy interferometru z fotodiody odpowiadają odcinkom drogi pryzmatu równym 0,5 l fali lasera. Oryginalnie rozwiązano konstrukcję części mechanicznej komory próżniowej. Jej osłona wykonana została w kształcie przezroczystej kwarcowej rury szklanej, o średnicy 200 mm i długości 400 mm, zamkniętej dwiema duraluminiowymi pokrywami. Podrzucanie reflektora odbywa się za pomocą linki gumowej, na której jest on zawieszony. Napinanie tej linki wykonuje silniczek elektryczny umieszczony na zewnątrz klosza. Na jego osi nawijana jest struna metalowa. Katapulta zwalniana jest po scentrowaniu reflektora za pomocą dźwigni połączonych z elektromagnesem. Konstruktor aparatu zastosował wiele własnych wynalazków w budowie części mechanicznej. Do najważniejszych zaliczyć trzeba sprężynowy tłumik drgań linki gumowej po podrzuceniu pryzmatu oraz regulator napięcia linki. Zastosowano odległość między poziomami rejestracji równą 2000 l fali interferencji, czyli 0,63 mm. Obserwacje wyrównywane są osobno po obydwu stronach krzywej balistycznej. Stosuje się przy tym funkcję zależności drogi od czasu w postaci:
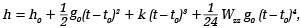
gdzie k jest parametrem redukcji ze względu na ciśnienie reszty powietrza w kloszu próżniowym. Wyrównane g0 odnosi się do szczytu toru, czyli do wysokości ok. 0,354 m nad poziomem znaku grawimetrycznego. Obserwacje powtarzane są automatycznie, co 15-20 s. Z serii dobowej uzyskuje się ciężkość z błędem średnim rzędu 0,02 mm•s-2 = 2 mGal.
Zasada względnych pomiarów grawimetrami statycznymi
W przypadku pomiaru przyspieszenia siły ciężkości metodą statyczną obserwacje dotyczą ustalenia położenia masy znajdującej się w stanie równowagi w systemie pomiarowym instrumentu. Jak podano w pierwszej części niniejszego opracowania, działanie siły ciężkości na masę systemu równoważone jest deformacją sprężyn pomiarowych lub kompensującego przesunięcie masy czujnika pola magnetycznego w przypadku grawimetrów nadprzewodnikowych.
Deformację liniową sprężyny Dz wywołuje różnica wartości przyspieszenia siły ciężkości Dg między punktami pomiarowymi P1 i P2. Jeżeli masa pomiarowa spełnia warunek stałości m = const, to w liniowym przybliżeniu otrzymuje się:
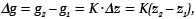
przy czym K oznacza współczynnik skali, nazywany stałą kalibracyjną lub współczynnikiem równania grawimetru. Ta idea wagi sprężynowej, służącej do pomiarów zmian przyspieszenia, wykorzystana została w konstrukcji grawimetrów morskich i w grawimetru marki GS-3 zbudowanego w połowie XX w. przez Niemca A. Grafa.
Natomiast zasada stosowania pomiaru kąta obrotu Da ramienia systemu mierzącego przy zmianie siły ciężkości wykorzystana została przy konstrukcji grawimetrów LaCoste & Romberg. Biorąc pod uwagę materiał użyty do konstrukcji systemu pomiarowego, współcześnie budowane mechaniczne grawimetry dzieli się na metalowe i kwarcowe. Elementy sprężyste wykonane są w kształcie sprężyn płaskich lub spiralnych. Odczyt skali grawimetru wykonywany jest na zasadzie „zerowania wskazań” instrumentu. Śrubą pomiarową licznika grawimetru doprowadza się ramię systemu mierzącego do położenia wyjściowego, najczęściej poziomego, na każdym stanowisku. Skala w okularze (woltomierza, czujnika elektronicznego) służy do ustalania położenia wskaźnika w położeniu „zerowym” skali.
Zarówno liniowe, jak i obrotowe systemy mierzące mogą być astatyzowane lub nieastatyzowane (ástatos po grecku oznacza niestały). W systemach „sprężynowo astatyzowanych” efekt zwiększenia czułości uzyskuje się przez zainstalowanie dodatkowej sprężyny, która zwiększa efekt zmian przyspieszenia siły ciężkości we wskazaniach grawimetru.

Grawimetr LaCoste-Romberg
Przy budowie systemu pomiarowego grawimetru marki LaCoste & Romberg z nieliniowym momentem sił sprężystych sprężyny astatyzującej zastosowano klasyczną już dzisiaj astatyzację przez umieszczenie nachylonej (ukośnej) sprężyny głównej. Konstruktor grawimetru L.J. LaCoste zastosował sprężynę o „zerowej” długości, której działanie astatyzujące znacznie powiększa obrót masy próbnej. Produkcja takiej sprężyny polega na skręcaniu nici w czasie nawijania na formę walcową. Sprężyna stwarza możliwość symetrycznych obrotów Da ramienia systemu pomiarowego względem położenia wyjściowego. Sposób rejestracji deformacji czujnikowych elementów systemu mierzącego pozwala wyróżnić grawimetry z optycznym urządzeniem do obserwacji wskaźnika położenia masy lub z systemem elektrycznym. Współcześnie produkowane grawimetry precyzyjne posiadają fotoelektryczne systemy rejestra cyjne. Wykorzystuje się przy tym zmiany prądu z fotokatody wywołane zmianami deformacji systemu pomiarowego.
Od 1987 r. firma Scintrex Co. produkowała grawimetry Autograv CG-3, a od 2004 – Autograv CG-5, sprzężone z wbudowanymi mikrokomputerami. Jako przenośny system pozyskiwania i kontroli danych zastosowano konsolę sterującą. System pomiarowy wykonany jest z kwarcu i pracuje w myśl zasady sejsmografu Golicyna. Masa próbna zawieszona jest na sprężynach kwarcowych, przemieszcza się przy zmianie przyciągania w polu elektrycznym między okładkami kondensatora. Zmiany pojemności elektrycznej przetwarzane są przez przetwornik pojemnościowo-przemieszczeniowy i rejestrowane automatycznie. Przetwornik ma rozdzielczość równą 0,2 nm. Układ sprzężenia zwrotnego przesuwa masę do pozycji wyjściowej (zerowej). Zmiany napięcia – równoważne zmianom grawitacji – transmitowane są do systemu zbierania danych i przetwarzane na sygnał cyfrowy do licznika. Jego wskazania wyświetlane są na ekranie z ciekłego kryształu – w wersji CG-3M (microGal resolution) z precyzją do 0,01 mm•s-2. Komputer grawimetru (48kb RAM) może zapamiętać odczyty na ok. 450 stanowiskach.
Przed pomiarem do pamięci komputera za pomocą klawiatury (14 dwufunkcyjnych klawiszy) wprowadza się współrzędne stanowiska. Komputer ma zegar kwarcowy, który wspomaga automatyczną eliminację liniowej części dryftu. Również automatycznie uwzględniany jest wpływ przyciągania Słońca i Księżyca. Szybkość zmian czasowych odczytu programuje się po zbadaniu grawimetru przed rejsem pomiarowym. Można także zaprogramować korektę termiczną wskazań. Ponadto naczynie próżniowe z sensorem grawitacyjnym, zespół elektroniczny i sensor pochylenia instrumentu umieszczone są w podwójnie termostatyzowanym pojemniku. Grawimetr nie ma mechanicznej kompensacji zmian temperatury. Kompensacja następuje za pomocą podzespołów elektronicznych. Instrument pracuje w zakresie temperatur od -40° do +45°C. Ma dwie libele elektroniczne o czułości ok. 1˝. Automatyczna korekcja błędów poziomowania jest wykonywana w zakresie + 200˝. Układ elektroniczny ma własny system autokalibracji wewnętrznej. Natomiast wartości współczynników w równaniu grawimetru są wprowadzane do pamięci komputera.
Pomiar odbywa się poprzez rejestrację położenia masy próbnej co sekundę w okresie zaprogramowanym przez obserwatora. Obserwator może również włączyć elektroniczny filtr sejsmiczny, eliminujący sygnały znacznie odbiegające od przeciętnej w próbkowaniu grawitacji. Wyświetlona zostaje średnia ciężkość referencyjna z całego okresu próbkowania, poprawiona ze względu na pływy grawitacyjne, nachylenie systemu i liniową część dryftu. Jeżeli odczyt i dziewięć innych zmiennych (średni moment obserwacji, poprawka pływowa, nachylenia w dwóch prostopadłych kierunkach, nr stanowiska, nr obserwatora, wskazania termometru, liczba próbek wziętych do średniej, liczba próbek odrzuconych i odchylenie standardowe) zostanie wprowadzonych do pamięci komputera, to po zakończeniu pomiarów istnieje możliwość ich transmisji do PC przez telefon lub modem i wydruku w formie dziennika obserwacji. Możliwy jest również wydruk daty i innych wprowadzonych danych o stanowisku. Grawimetr ma zasięg ok. 70 000 µm•s-2, nie wymaga przestawiania zakresu na całym globie. Jego wymiary to: 0,24×0,31×0,32 m, a masa z akumulatorem – blisko 11 kg. Nie ma aretażu systemu pomiarowego. W Polsce (a także m.in. w Chinach i Jordanii) używano grawimetru Autograv CG-3M do pomiaru części podstawowej sieci grawimetrycznej kraju.
Poniżej parę uwag dotyczących teorii działania grawimetrów statycznych. Najszerzej stosowane są obecnie grawimetry z systemem pomiarowym, w którym masa ma możliwość obrotu wokół osi. System ma więc jeden stopień swobody. W chwili, gdy system znajduje się w równowadze, suma wszystkich sił równa jest zeru. Jeśli moment inercji systemu jest M(a), to moment sił zewnętrznych wynosi g/M(a). Moment sił wewnętrznych, sprężystych, przeciwdziałających zmianom ciężkości wynosi N(a). Równanie równowagi systemu pomiarowego grawimetru będzie przedstawiało się następująco:
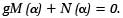
Do sił zewnętrznych zalicza się wpływ temperatury t, ciśnienia atmosferycznego B, zmian przyspieszenia g i kąta b nachylenia osi obrotu ramienia masy próbnej. Moment siły sprężystości materiału, z którego wykonany jest system mierzący, zależy od stopnia deformacji układu, od temperatury wewnętrznej, a także od czasu t, który upłynął od wyprodukowania i uruchomienia grawimetru, czyli od „wystarzenia” systemu. Ostatnie równanie można zatem zapisać w postaci:
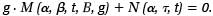
Gdy równanie to podda się zróżniczkowaniu, to uzyskany współczynnik Da/Dg charakteryzuje deformacje systemu na skutek zmian przyspieszenia. Jest to tzw. czułość układu. Grawimetr jest tym wyższej jakości, im wyższą posiada czułość i im mniej wskazania grawimetru zależą od zmian temperatury i ciśnienia atmosferycznego. Obsługę ułatwia mała zależność wskazań od kąta pochylenia, ponieważ instrument taki wymaga mniej dokładnego poziomowania i mniej dokładnej rektyfikacji libel.
Opracowanie wyników pomiarów grawimetrami statycznymi jest prostsze niż w przypadku grawimetrów dynamicznych. Niewątpliwą wadą tego rodzaju grawimetrów jest większy chód (dryft), czyli zmiana odczytów z upływem czasu (również bez zmiany miejsca pomiaru), w porównaniu z chodem aparatu dynamicznego. Wymaga to ograniczenia czasu trwania rejsu pomiarowego do kilku godzin i prawidłowego modelowania poprawek chodowych. Grawimetry statyczne wymagają też kalibracji (skalowania, cechowania). Mają zazwyczaj ograniczony zasięg pomiarowy (tzw. zakres). Zależnie od przeznaczenia waha się on w granicach od kilkunastu mm/s-2 (grawimetry małozakresowe) do kilku tysięcy mm/s-2 (grawimetry szerokozakresowe, geodezyjne). W zasadzie z powiększeniem zakresu grawimetru maleje dokładność pomiaru Dg.
Zmiany równania grawimetru spowodowane są zmianą szerokości geograficznej (ściślej – zmianą przyspieszenia siły ciężkości) i występują przede wszystkim po zmianie zakresu w grawimetrach małozakresowych. Cechowanie (skalowanie, kalibrowanie, komparacja) grawimetru polega na ustaleniu związku między zmianą przyspieszenia siły ciężkości Dg a zmianą odczytu DS instrumentu. Przy wyznaczaniu współczynnika (stałej) K grawimetru statycznego należy uwzględnić temperaturę przyrządu, upływ czasu między powtórnymi obserwacjami na stanowisku wyjściowym (czyli chód grawimetru), wpływ sił pływowych, nieliniowość równania grawimetru, zmiany ciśnienia atmosferycznego i inne systematyczne czynniki. W zależności od sposobu realizacji wzorcowej wartości Dg służącej do obliczenia stałej w myśl wzoru:
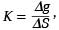
rozróżnia się kilka metod skalowania, a mianowicie:
- cechowanie (kalibracja) na bazach grawimetrycznych,
- cechowanie przez nachylanie na egzaminatorze,
- skalowanie przez przybliżanie do ciężaru,
- kalibracja przez obciążanie dźwigni systemu mierzącego.
Ramy niniejszego opracowania nie pozwalają na szersze omówienie metod kalibracji. Podajmy przeto jedynie wskazówkę, że odcinek bazy grawimetrycznej wybrany do skalowania grawimetru powinien rozciągać się w kierunku południkowym na długości obejmującej badany fragment terenu, by następnie pomiar różnic przyspieszenia wykonać bez przestawiania zakresu.
W 1968 r. W. Prothero i J. Goodkind zbudowali w San Diego (USA) pierwszy grawimetr statyczny, którego zasada działania wykorzystuje zjawisko nadprzewodności metali. Konstrukcja instrumentu polega na zamianie siły mechanicznej podtrzymującej element pomiarowy grawimetru w położeniu równowagi na siłę pola magnetycznego. Jest to możliwe wtedy, gdy element ten wykonany jest z nadprzewodnika i umieszczony zostanie w stałym polu magnetycznym. Przebieg linii sił tego pola dobierany jest w zależności od kształtu próbnika w taki sposób, by linie sił indukcji nie przenikały do jego wnętrza. Oddziaływanie występujące między stałym polem magnetycznym a prądami wirowymi na powierzchni elementu pomiarowego nosi nazwę zjawiska Meissnera-Ochsenfelda. Jego istota polega na tym, że prądy wirowe na powierzchni nadprzewodnika wytwarzają pole magnetyczne, które zupełnie kompensuje działanie zewnętrznego pola magnetycznego w elemencie pomiarowym. Prądy wirowe zanikają, czyli linie sił zewnętrznego pola magnetycznego nie mogą przeniknąć do wnętrza próbnika. Jeżeli naprzewodzący element pomiarowy umieszczony zostanie w polu magnetycznym i ochłodzony do temperatury krytycznej (ok. 6°K), przy której następuje przemiana fazowa w stan nadprzewodności, to pole magnetyczne w tym momencie zaniknie w bryle próbnika.
Dodajmy kilka szczegółów o budowie grawimetru nadprzewodnikowego. We wnętrzu naczynia próżniowego znajduje się próbnik z nadprzewodnika w kształcie sfery. Pole magnetyczne zewnętrzne wytwarzane jest przez prąd elektryczny przepływający przez solenoidy wykonane z nadprzewodnika. Sfera lewituje między dwoma magnesami, umieszczonymi w pionie nad i pod sferycznym próbnikiem. Zmiana siły ciężkości wywoła zmianę położenia sfery i zmianę pojemności elektrycznej między sferą i magnesami. Specjalny czujnik przetwarza zmianę pojemności na impuls elektryczny i przesuwa sferę w położenie wyjściowe przez elektromagnetyczny układ sprzężony (zwrotny). Zmiany natężenia na kondensatorze sprzężenia zwrotnego są miarą zmian przyspieszenia siły ciężkości. Grawimetr ma zaniedbywalny dryft, bo ok. 0,01 mm/s-2 na miesiąc. Nie wymaga kalibracji. Do połowy lat 90. wykorzystywano grawimetry nadprzewodnikowe jako instrumenty stacjonarne tylko do rejestracji pływowych zmian siły ciężkości i wpływu ruchu biegunów Ziemi na grawitację.
Firma amerykańska GWR Instruments z San Diego od 1995 r. produkuje precyzyjne, przenośne (waga ok 15 kg, rozmiary: 60 cm wysokości, 30 cm średnica) grawimetry nadprzewodnikowe. Pojemnik chłodzący takiego instrumentu zawiera ciekły hel. Wymiana 8 litrów helu musi następować co 7 dni. Dryft instrumentu jest nie większy niż 0,01 mm/s-2 na tydzień, a powtarzalność odczytów – ok. 0,001 mm/s-2. W grawimetry tego typu wyposażone są liczące się na świecie obserwatoria pływowe. W 1997 r. zainstalowano do monitorowania pływów ziemskich w obserwatorium satelitarno-geodynamicznym w Wettzell (Niemcy) grawimetr nadprzewodnikowy GWR marki CD z dwiema sferami lewitującymi. Jego system pomiarowy posiada dwa nadprzewodzące czujniki grawitacyjne. Średnica każdej ze sfer wynosi 1 cal = 2,54 cm. Temperatura we wnętrzu termosu jest utrzymywana w granicach do 3,2 K. Dryft tego grawimetru nie przekracza ok. 65 nm/s-2/rok.
Uwagi końcowe
Przedstawiony powyżej materiał nie wyczerpuje, rzecz jasna, nawet skrótowych wiadomości z zakresu metodyki i technologii grawimetrii geodezyjnej. Zainteresowanych poruszoną tu tematyką odsyłamy do podręcznikowej pozycji [Torge, 1989] i książki autora [Barlik, 2001]. Tam znajdzie Czytelnik także wybrane zagadnienia z zakresu pomiarów wyższych pochodnych potencjału siły ciężkości (pomiary gradientometryczne) oraz pomiarów inercjalnych. Nie podaliśmy tutaj także elementarnych wiadomości z działu grawimetrii satelitarnej – dynamicznej. Do zakresu grawimetrii geodezyjnej zalicza się ponadto badania zmian kierunku pionu metodami inklinometrycznymi, niewyjaśnionymi w tym artykule. O zastosowaniu wyników informacji grawimetrycznych m.in. w opracowaniu pomiarów niwelacyjnych pisaliśmy w GEODECIE w pozycji [Barlik i inni, 1999]. W następnym opracowaniu mamy zamiar przedstawić natomiast prace wykonane przy użyciu nowoczesnego grawimetru balistycznego FG-5, zainstalowanego w laboratorium grawimetrycznym Politechniki Warszawskiej.
Prof. Marcin Barlik był pracownikiem Instytut Geodezji Wyższej i Astronomii Geodezyjnej Politechniki Warszawskiej
Recenzent: dr Andrzej Sas był pracownikiem Instytutu Geodezji i Kartografii w Warszawie
Literatura:
- Barlik M., 1991: Normalna ciężkość dla obszaru Polski w globalnych systemach odniesienia, „Przegląd Geodezyjny”, t. LXIII, nr 9;
- Barlik M., 2001a: Pomiary grawimetryczne w geodezji, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa;
- Barlik M., 2001b: Wykorzystanie pionowego gradientu ziemskiej siły ciężkości w niektórych zagadnieniach geodezyjnych, GEODETA 5/2001 (cz. I) i 6/2001 (cz. II);
- Barlik M., Chruślińska M., 1999: O systemach niwelacji geometrycznej, GEODETA 4/1999;
- Morelli C. i inni, 1974: The International Gravity Standardization Net 1971 (IGSN’71), Bureau Central International Association of Geodesy, Paris;
- Sas-Uhrynowski, 2002: Absolute gravity measurements in Poland, Institute of Geodesy and Cartography, Monographic Series, No. 3, Warszawa;
- Sas-Uhrynowski A., Cisak M., Sas A., Siporski L, 1999: Zmodernizowana podstawowa osnowa grawimetryczna kraju (POGK’97), „Prace IGiK”, t. XLVI, z. 98, Warszawa;
- Siporski L, 1999: Wyrównanie wyników pomiarów nowej podstawowej osnowy grawimetrycznej kraju (POGK’97), „Prace IGiK”, t. XIV, z. 98, Warszawa;
- Torge W., 1989: Gravimetry. W. de Gruyter, Berlin – N. York;
- Ząbek Z., 1996: The transpotable ballistic gravimeter ZZG, „Reports on Geodesy”, No. 3(21), Warsaw University of Technology, Institute of Geodesy and Geodetic Astronomy, Warsaw.
Opracowanie zamieszczono na Geoforum w styczniu 2007 r.
|
