|
Jan Kryński
Z ogólnej teorii względności wynika, że czas nie jest bezwzględny. Płynie on w różny sposób w różnych systemach odniesienia, komplikując tym samym ich definicje.
Niedoskonałość definicji niebieskich systemów odniesienia i ich relacji z systemem ziemskim częściowo eliminowano poprzez stosowanie tzw. poprawek relatywistycznych, traktowanych jako zakłócenia newtonowskiego modelu mechaniki (Kovalevsky, 2002). Coraz wyraźniej rysowała się jednak potrzeba zdefiniowania niebieskich systemów odniesienia w ujęciu mechaniki relatywistycznej w abstrakcyjnej czterowymiarowej czasoprzestrzeni z użyciem układu współrzędnych (x0 = ct, x1, x2, x3), gdzie c jest prędkością światła w próżni, a t – tzw. czasem współrzędnych.
Nieinercjalny system odniesienia
Ponieważ w praktyce definiowalne mogą być jedynie przybliżenia systemów inercjalnych, należało skorzystać z nieinercjalnego systemu odniesienia. W nieinercjalnym systemie odniesienia geometria czasoprzestrzeni określona jest przedstawioną przy użyciu konwencji Einsteina (Trajdos-Wróbel, 1966) uogólnioną formą kwadratową (Landau i Lifszyc, 1980):
ds2 = –c2dτ2ds2 = –c2dτ 2 = gikdxidxk, (1)
gdzie τ jest tzw. czasem własnym (nazywanym również czasem prawdziwym) danego punktu w przestrzeni, zaś współczynniki gik (i, k = 0, 1, 2, 3) są pewnymi funkcjami współrzędnych przestrzennych x1, x2, x3 i współrzędnej czasowej x0. Układ współrzędnych
(x0 = ct, x1, x2, x3) w nieinercjalnym systemie odniesienia
(gik różnego od 0 oraz różnego od k) nie jest już układem kartezjańskim, tylko krzywoliniowym. Współczynniki gik formy kwadratowej (1) określają wszystkie własności geometrii w dowolnym krzywoliniowym układzie współrzędnych i ustalają metrykę czasoprzestrzeni. Są one składowymi tensora metrycznego i zachowują tę samą wartość we wszystkich układach współrzędnych. Interwał ds z formalnego punktu widzenia może być traktowany jako odległość dwóch punktów w abstrakcyjnej czterowymiarowej przestrzeni z wprowadzoną przez Minkowskiego geometrią pseudoeuklidesową. W określeniu relacji pomiędzy systemami odniesienia zasadniczą rolę odgrywa rodzaj przestrzeni, w której zdefiniowane są systemy, oraz zachowanie niezmienności interwału ds między zdarzeniami.
ICRS i ICRF
Nowy niebieski system odniesienia przyjęty został przez XXIII Zgromadzenie Generalne IAU w Kyoto w 1997 roku. Od 1 stycznia 1998 roku stał się on obowiązującym systemem IAU (IAU, 1999) jako Międzynarodowy Niebieski System Odniesienia ICRS (International Celestial Reference System). Kinematyczną realizacją ICRS, przeznaczoną do zastosowań praktycznych, jest Międzynarodowy Niebieski Układ Odniesienia ICRF (International Celestial Reference Frame). Jednocześnie Katalog Hipparcos, który powstał na podstawie obserwacji astrometrycznych wykonanych w ramach misji satelity Hipparcos (Perryman i in., 1997), został zatwierdzony jako podstawowa realizacja ICRS w zakresie widma optycznego.
ICRF został zdefiniowany z dokładnością około 30 µas (as – sekunda łuku) poprzez pozycje 212 definiujących radioźródeł określone na podstawie obserwacji VLBI (IAU, 1996). Konwencjonalny (Umowny) Biegun Odniesienia CRP (Conventional Reference Pole) systemu ICRS (kierunek prostopadły do podstawowej płaszczyzny układu) oparty jest na modelu precesji IAU1976 (Lieske i in., 1977) i teorii nutacji IAU1980 (Wahr, 1981). Jest on bardzo zbliżony do średniego bieguna Katalogu FK5 na epokę J2000.0. Punkt początkowy liczenia rektascensji w ICRS, który określa kierunek osi x1 tego systemu, niemal pokrywa się z punktem równonocy wiosennej Katalogu FK5 (Kołaczek, 2004; Kryński, 2004a).
System barycentryczny i geocentryczny
Jednocześnie z definicją systemu ICRS zaistniała potrzeba zdefiniowania w ujęciu ogólnej teorii względności kilku układów współrzędnych (x0 = ct, x1, x2, x3) w czasoprzestrzeni w taki sposób, aby w każdym układzie współrzędnych o początku w barycentrum dowolnego zbioru mas kwadrat interwału ds między zdarzeniami był wyrażony z odpowiednim stopniem przybliżenia poprzez współczynniki gik w (1) (Kryński, 2004a). Ostatecznie przyjęto definicje barycentrycznego systemu odniesienia i geocentrycznego systemu odniesienia, którym odpowiednio nadano nazwy:
- Barycentryczny Niebieski System Odniesienia BCRS (Barycentric Celestial Reference System) o początku w środku mas Układu Słonecznego z czasem współrzędnych barycentrycznych TCB (Barycentric Coordinate Time),
- Niebieski Geocentryczny System Odniesienia GCRS (Geocentric Celestial Reference System) o początku w środku mas Ziemi z czasem współrzędnych geocentrycznych TCG (Geocentric Coordinate Time).
Systemy te, które łącznie tworzą system ICRS (Kovalevsky, 2002), sformułowane zostały z uwzględnieniem współczesnego formalizmu ogólnej teorii względności oraz przy użyciu oceny harmonicznej, z zaleceniem, aby:
- układy te nie podlegały obrotom względem zbioru odległych obiektów pozagalaktycznych,
- współrzędne czasowe tych układów były wyprowadzone ze skali czasu realizowanej przez działające na Ziemi zegary atomowe,
- jednostkami fizycznymi w tych układach były jednostki SI.
Dla obu niebieskich systemów odniesienia zdefiniowano współczynniki gik (1) jako funkcje sumy potencjału grawitacyjnego zbioru mas określających odpowiednio barycentrum Układu Słonecznego i środek mas Ziemi oraz generowanego przez ciała zewnętrzne względem tych zbiorów potencjału pływowego zanikającego odpowiednio w barycentrum lub w środku mas Ziemi (IAU, 2001; Kryński, 2004a). Za czas odniesienia dla widomych (pozornych) geocentrycznych efemeryd przyjęto Czas Ziemski TT (Terrestrial Time) – czas własny systemu geocentrycznego oraz określono relację między TCG i TT. Sformułowano również pełną postnewtonowską czterowymiarową transformację pomiędzy systemami BCRS i GCRS, zwaną uogólnioną transformacją Lorentza (Kovalevsky, 2002), narzuconą przez formę odpowiednich tensorów metrycznych. Obejmuje ona w szczególności transformację pomiędzy skalami czasów współrzędnych TCB i TCG. W celu zachowania ciągłości w pozycjach gwiazd przy zmianie systemu FK5 na nowy barycentryczny system odniesienia dodatkowo zalecono, aby ten ostatni był możliwie bliski równikowi i punktowi równonocy wiosennej FK5 odniesionym do epoki J2000.0. A zatem podstawowa płaszczyzna tego układu (płaszczyzna x1x2 odpowiadająca płaszczyźnie równika niebieskiego w katalogowych układach odniesienia), określona przez Konwencjonalny (Umowny) Biegun Odniesienia CRP (Conventional Reference Pole), zwany również biegunem ICRF, znajdować się ma możliwie blisko płaszczyzny średniego równika na epokę J2000.0. Z kolei punkt początkowy układu (odpowiednik punktu równonocy wiosennej w katalogowych układach odniesienia, czyli kierunek osi x1, od którego odmierzana jest rektascensja) – znajdować się winien blisko dynamicznego punktu równonocy wiosennej na epokę J2000.0.
CTRS a ITRS
Ziemski system odniesienia jest kinematycznym geocentrycznym systemem przestrzennym obracającym się wraz z Ziemią. W systemie tym pozycje punktów związanych z powierzchnią Ziemi określone są przez współrzędne, które podlegają jedynie małym zmianom w czasie spowodowanym przez efekty geofizyczne (ruchy tektoniczne, deformacje pływowe). Ziemski układ odniesienia – określony przez zbiór punktów o precyzyjnie wyznaczonych współrzędnych w systemie współrzędnych powiązanych z ziemskim systemem odniesienia – jest realizacją ziemskiego systemu odniesienia. CTRS – zgodnie z definicją (IAG, 1992) – jest quasi-kartezjańskim systemem zdefiniowanym przez przestrzenny obrót względem nieobracającego się systemu geocentrycznego GCRS z dokładnością na poziomie milimetrowym. Czasem współrzędnych CTRS jest TCG – czas współrzędnych GCRS. Początkiem CTRS jest środek mas Ziemi z uwzględnieniem oceanów i atmosfery. CTRS nie podlega globalnemu, residualnemu obrotowi względem ruchów poziomych na powierzchni Ziemi.
ITRS, czyli CTRS monitorowany przez IERS, jest systemem geocentrycznym, którego jednostką długości jest metr SI. System ITRS różni się jednak zasadniczo od CTRS. W przeciwieństwie do CTRS jest on zdefiniowany w trójwymiarowej przestrzeni euklidesowej. W myśl postanowień IUGG i IAU (1991 r.) skala systemu ITRS jest spójna z czasem współrzędnych geocentrycznych TCG. Składowa czasowa ITRS reprezentowana jest przez epokę systemu. Uproszczenie definicji ITRS w stosunku do definicji CTRS zachowuje dokładność systemu na poziomie milimetrowym. Orientacja ITRS jest zgodna z orientacją BIH 1984.0, zaś jej zmienność w czasie jest określona poprzez zastosowanie warunku, iż globalna suma poziomych ruchów tektonicznych nie zawiera składowych obrotu.
ITRF i systemy regionalne
Realizacjami ITRS są Międzynarodowe Ziemskie Układy Odniesienia ITRF (International Terrestrial Reference Frame). Do 1993 roku początki układów ITRF (włącznie z ITRF93) i ich skale wyznaczane były na podstawie wybranych rozwiązań satelitarnych obserwacji laserowych. Układy te orientowano zgodnie z ziemskim systemem BTS87 opartym na parametrach ruchu obrotowego Ziemi wyznaczanych przez BIH (do orientacji ITRF93 użyto parametrów ruchu obrotowego Ziemi IERS). Zmiany orientacji w ITRF w czasie określano początkowo na podstawie modelu ruchu płyt tektonicznych AM0-2 (Minster i Jordan, 1978), a od 1991 roku – na podstawie modeli NNR-NUVEL-1, NNR-NUVEL-1A (Argus i Gordon, 1991), z wyjątkiem ITRF93 (IERS, 2003).
Już od ITRF94 początki układów ITRF wyznaczane są jako średnia ważona rozwiązań SLR i GPS, zaś skala układów określana jest jako średnia ważona rozwiązań VLBI, SLR i GPS, poprawiona o 0.7 ppb (1 ppb = 1 x 10-9) z uwagi na używanie przez centra analiz skali czasu TT zamiast zaleconej przez IAU i IUGG skali TCG. Układy te są zorientowane zgodnie z ITRF92. Zmiany orientacji określone są na podstawie modelu NNR-NUVEL-1A i wyrażone jako pochodne względem czasu 7 parametrów transformacji (IERS, 2003). Orientacja ITRF i zmiany tej orientacji określają równik ITRF (a tym samym biegun ITRF) oraz południk zerowy ITRF.
Rozszerzeniem ITRS są regionalne systemy odniesienia wpasowane w ITRS. Przykładem takiego systemu jest European Terrestrial Reference System 89 (ETRS89), którego realizacja oparta jest na obserwacjach wyłącznie z europejskich stacji permanentnych. ETRS89 został zdefiniowany jako pokrywający się z ITRS na epokę 1989.0 i związany ze stabilną częścią płyty euroazjatyckiej. Realizacją ETRS89 jest układ odniesienia European Terrestrial Reference Frame 89 (ETRF89), który jest obecnie w większości krajów europejskich – w tym również w Polsce – państwowym geodezyjnym przestrzennym układem odniesienia stosowanym w pracach geodezyjnych oraz w systemach informacji o terenie.
Pośredni System Odniesienia IRS
Istotnym elementem współczesnych systemów odniesienia stał się tzw. Pośredni System Odniesienia IRS (Intermediate Reference System). Ten geocentryczny system podlega obrotom zarówno względem GCRS, którego kierunki osi pozostają ustalone w przestrzeni, jak i względem ITRS sztywno w sensie kinematycznym związanego z Ziemią. Uwzględnienie tych dwóch typów obrotów leży u podstaw definicji systemu IRS. Jedną z zasadniczych zmian, jaka została wprowadzona w definicji niebieskich systemów odniesienia, a która została zmaterializowana w definicji IRS, jest zastąpienie punktu równonocy wiosennej – jako początku liczenia rektascensji – znacznie wygodniejszym w użyciu i dokładniej zdefiniowanym punktem na równiku. Stosowanie ruchomego (zmiennego w czasie) punktu równonocy jako punktu odniesienia nie jest konieczne i komplikuje opis relacji pomiędzy systemami odniesienia (Guinot, 1979). Co więcej, na współczesne obserwacje (VLBI i SLR) służące do wyznaczania parametrów orientacji Ziemi w przestrzeni praktycznie nie ma wpływu orientacja ekliptyki i ruch punktu równonocy (Capitaine i Guinot, 1988). W dodatku stosowane modele systemów odniesienia nie uwzględniały w wyrażeniu na prawdziwy czas gwiazdowy Greenwich GST (Greenwich Sidereal Time) pewnych mieszanych wyrazów precesyjno-nutacyjnych, o wielkościach dochodzących do 0.001 as, które odpowiadały precyzji obserwacji. Teoria „nieobracającego się punktu początkowego” NRO (Non-Rotating Origin) na ruchomym równiku (Guinot, 1979), oparta na nieobracającym się systemie odniesienia, została wykorzystana do zdefiniowania pośredniego systemu odniesienia.
Ruch CIP względem GCRS
Podstawową oś systemu IRS definiuje Pośredni Biegun Niebieski CIP (Celestial Intermediate Pole) – niemal pokrywający się z CEP (Celestial Ephemeris Pole) systemu katalogu FK5 na epokę J2000.0. Oś CIP dokonuje ruchu precesyjno-nutacyjnego wokół osi bieguna C0 systemu GCRS (w ogólności ICRS) – rys. 1.
Definicji IRS obowiązującej od 1 stycznia 2003 roku towarzyszy przyjęta przez IAU (IAU, 2001) nowa teoria precesyjno-nutacyjna IAU2000 (Brzeziński, 2004). Zgodnie z nią ruch CIP (będącego biegunem IRS) względem GCRS jest określony poprzez ruch średniej osi Tisseranda Ziemi (Seidelmann, 1982), zawierający okresy dłuższe niż dwa dni. Kierunek CIP na epokę J2000.0 jest nieznacznie przesunięty względem kierunku bieguna GCRS, w sposób zgodny z modelem precesyjno-nutacyjnym IAU2000A (Dehant i in., 1999).
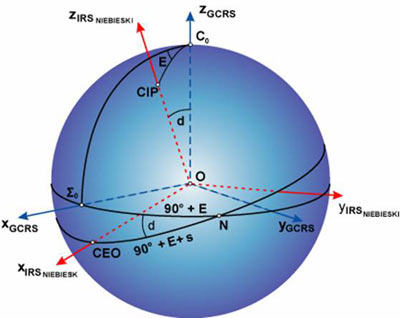
Rys. 1. Relacja pomiędzy systemami GCRS i IRS
(O – środek mas Ziemi, Σ0 – punkt początkowy liczenia rektascensji w systemie GCRS, N – węzeł wstępujący równika CIP z równikiem bieguna C0 systemu GCRS)
Ruch CIP względem GCRS realizowany jest poprzez model precesyjno-nutacyjny IAU2000A dla okresów dłuższych niż dwa dni, z dodatkowym uwzględnieniem zależnej od czasu poprawki wyznaczanej przez IERS na podstawie obserwacji astronomiczno-geodezyjnych. Kąty d i E opisują ruch precesyjno-nutacyjny CIP względem C0. Jako niebieski początek efemerydalny przyjęto „nieobracający się punkt początkowy” w GCRS i desygnowano ten punkt jako Niebieski Efemerydalny Punkt Początkowy CEO (Celestial Ephemeris Origin) na równiku CIP. Położenie CEO może być obliczone na podstawie modelu IAU2000A precesji i nutacji CIP oraz na podstawie obecnych wartości przesunięcia CIP względem bieguna ICRF na epokę J2000.0 przy użyciu wzorów opracowanych przez (Capitaine i in., 2003). Wykorzystywane są do tego celu kąty d i E oraz wielkość s, określająca zmianę położenia punktu CEO na chwilowym równiku spowodowaną przez ruch bieguna CIP względem systemu niebieskiego GCRS. W tak zdefiniowanym Pośrednim Systemie Odniesienia – nazwanym IRSNIEBIESKI (Kryński i Sękowski, 2004; Kryński, 2004b) – punkt CEO służy jako początek liczenia rektascensji. Pozycja gwiazdy określona w tym systemie odpowiada pozycji pozornej tradycyjnie używanej w odniesieniu do poprzednio stosowanych systemów, z tym że występująca pomiędzy nimi rosnąca w czasie od 2000 roku różnica w rektascensji wynosiła w połowie 2005 roku około 16.9 s (Kryński i Sękowski, 2004).
Ruch CIP względem ITRS
W definicji IRS, obok sprecyzowania ruchu CIP względem GCRS, określony jest ruch CIP względem ITRS. Ruch CIP względem ITRS wyznaczany jest przez IERS w formie ciągu czasowego (xP, yP) na podstawie odpowiednich obserwacji astronomiczno-geodezyjnych oraz przy użyciu modeli zawierających zmiany o wysokiej częstotliwości. Wyrazy nutacji wymuszonej o okresach krótszych od dwóch dni zawarte są w modelu ruchu CIP względem ITRS (Kryński, 2004b). Jako ziemski początek efemerydalny, który zastąpił punkt przecięcia równika CEP z prawdziwym południkiem Greenwich, przyjęto „nieobracający się punkt początkowy” w ITRS i desygnowano ten punkt jako Ziemski Efemerydalny Punkt Początkowy TEO (Terrestrial Ephemeris Origin) na równiku CIP. Położenie TEO jedynie w nieznacznym stopniu zależy od ruchu bieguna i może być ekstrapolowane zgodnie z wynikami opracowania (Capitaine i in., 2000), przy użyciu danych IERS.

Rys. 2. Relacje pomiędzy systemami ITRS, IRS ZIEMSKI i IRS NIEBIESKI
(O – środek mas Ziemi, ω0 – punkt początkowy liczenia długości w systemie ITRS, M – węzeł wstępujący równika CIP z równikiem bieguna R0 systemu ITRS)
W obracającym się wraz z Ziemią Pośrednim Systemie Odniesienia – nazwanym IRS ZIEMSKI (Kryński i Sękowski, 2004; Kryński, 2004b) – punkt TEO służy jako początek liczenia długości. Kąt pomierzony w płaszczyźnie równika CIP pomiędzy wektorami jednostkowymi skierowanymi od osi obrotu Ziemi do CEO i TEO zdefiniowano jako Kąt Obrotu Ziemi ERA (Earth Rotation Angle) – rys. 2.
Profesor Jan Kryński był kierownikiem Zakładu Geodezji i Geodynamiki w Instytucie Geodezji i Kartografii w Warszawie
Opracowanie 2006
| 