Regionalnie i lokalnie

Jan Kryński

Na podstawie pierwszych realizacji systemu ITRS przekonano się, iż stosowanie go jako systemu odniesienia dla potrzeb geodezyjnych poszczególnych krajów lub regionów nie jest wygodne w praktyce, z uwagi na znaczące różnice pomiędzy kolejnymi układami odniesienia ITRF. W wyniku inicjatywy podjętej na XIX Zgromadzeniu Generalnym IUGG w Vancouver w 1987 roku opracowano podstawy teoretyczne sieci kontynentalnych, które posłużyłyby za oparcie dla regionalnych układów odniesienia. Systemy takie, związane ze sztywną płytą tektoniczną, dzięki wyeliminowaniu lub istotnemu zmniejszeniu wpływu prędkości ruchów stacji zapewniają dokładniejsze wyznaczanie pozycji.

Europejski Ziemski System Odniesienia ETRS89

Dla kontynentu europejskiego regionalnym systemem odniesienia jest Europejski Ziemski System Odniesienia ETRS89 (European Terrestrial Reference System 89), którego realizację powierzono powołanej w tym celu podkomisji EUREF (European Reference Frame) Międzynarodowej Asocjacji Geodezji IAG. ETRS89 zdefiniowano jako system pokrywający się z ITRS na epokę 1989.0 i sztywno związany ze stabilną częścią płyty euroazjatyckiej. Dla zapewnienia zgodności realizacji tego systemu, tj. Europejskiego Ziemskiego Układu Odniesienia ETRF89 (European Terrestrial Reference Frame 89), z odpowiednią realizacją systemu ITRS do jego zdefiniowania wykorzystano sieć leżących w Europie stacji SLR i VLBI, wykorzystanych do realizacji układu ITRF89. W ten sposób ETRF89 stał się podzbiorem układu ITRF89. W wyniku ciągłego, wzajemnego ruchu płyt tektonicznych układ ETRF przemieszcza się w odniesieniu do układu ITRF z prędkością 1-3 cm/rok. Jednocześnie prawie nie ulega on deformacji wewnętrznej, poza lokalnymi ruchami tektonicznymi (Rogowski i Figurski, 2004).


ETRF89 na terenie Polski

W wyniku przeprowadzonej w 1992 r. kampanii GPS EUREF-POL92 do układu ETRF89 dowiązano 11 stacji na terenie Polski. Z kolei kampanie GPS przeprowadzone od lipca 1994 do maja 1995 roku dostarczyły materiału obserwacyjnego umożliwiającego wyznaczenie w układzie ETRF89 pozycji 360 stacji sieci POLREF – zagęszczającej punkty EUREF-POL92. Stosując punkty POLREF jako punkty odniesienia, przeliczono do układu ETRF89 pozycje punktów państwowej osnowy geodezyjnej I klasy (1996 r.), a następnie II klasy (1997 r.). Na podstawie rozporządzenia Rady Ministrów z 8 sierpnia 2000 r. ETRF89 jest obowiązującym w Polsce geodezyjnym układem odniesienia wchodzącym w skład państwowego systemu odniesień przestrzennych.

ETRF, podobnie jak ITRF, jest układem kinematycznym. Jego realizacja i utrzymanie wymaga ciągłego monitorowania za pośrednictwem odpowiednio rozmieszczonych permanentnych stacji GPS tworzących sieć EPN (EUREF Permanent GPS Network). Dokładne określenie zmian w czasie współrzędnych stacji wymaganych do nawiązania wykonanych w dowolnej epoce obserwacji GPS do obowiązującego układu ETRF89 możliwe jest jedynie wtedy, gdy odpowiednio blisko położone stacje permanentne prowadzą obserwacje w sposób ciągły. Dopiero wieloletnie ciągi obserwacji z danej stacji permanentnej, opracowywane wraz z danymi z innych stacji EPN, dostarczają dostatecznej informacji o zmienności współrzędnych stacji. Spośród 10 funkcjonujących w Polsce stacji EPN takimi wieloletnimi ciągami dysponują: BOGO (Borowa Góra), BOR1 (Borowiec), JOZE (Józefosław), LAMA (Lamkówko) i WROC (Wrocław). Odpowiednio rozmieszczone i sprawnie funkcjonujące stacje sieci EPN są niezbędne do wyrażenia w obowiązującym układzie ETRF89 wyników obserwacji wykonanych w aktualnie używanej realizacji systemu globalnego ITRS (obecnie ITRF2000). Rozmieszczenie stacji permanentnych IGS/EUREF w Polsce przedstawiono na rys. 1.

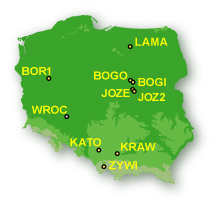
Rys. 1. Stacje permanentne sieci IGS/EUREF w Polsce (2004 r.)

Pomiary GPS: przejście od ITRF do ETRF89

Opracowanie orbit satelitów GPS oraz obliczanie efemeryd zarówno pokładowych, jak i precyzyjnych, odbywa się przy wykorzystaniu nie tylko niebieskich, ale także i ziemskich systemów odniesienia wraz z uwzględnieniem zachodzących między nimi relacji. Orbity satelitów GPS udostępniane są użytkownikom w aktualnym układzie ITRF. W ITRF wyznaczane są zatem współrzędne punktów z obserwacji GPS. Wyrażenie pozycji w obowiązującym układzie regionalnym, np. ETRF89, wymaga zastosowania odpowiedniej strategii i algorytmu z użyciem parametrów opracowanych przez służby międzynarodowe. Schemat strategii (Boucher, 1994) przejścia od aktualnej realizacji ITRF do układu ETRF89 pokazany jest na rys. 2.

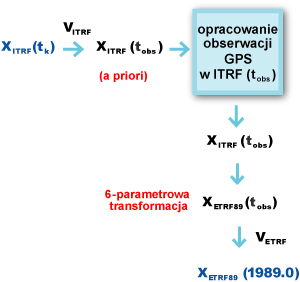
Rys. 2. Schemat strategii prowadzącej do wyznaczenia pozycji
w układzie ETRF89 na epokę 1989.0

Opracowanie obserwacji GPS poprzedza obliczenie a priori współrzędnych stacji w ITRF na epokę obserwacji t_obs na podstawie współrzędnych katalogowych tych stacji w ITRF na epokę t_k katalogu oraz wektora V_ITRF składowych prędkości tych stacji w ITRF. Składowe tego wektora można uzyskać z raportów IERS, zaś dla stacji nieumieszczonych w katalogach korzysta się do ich obliczenia z modelu geofizycznego ruchu płyt tektonicznych NNR-NUVEL-1A. Otrzymane w wyniku opracowania pomiarów GPS współrzędne stacji w ITRF na epokę obserwacji są następnie przeliczane do układu ETRF89 na epokę obserwacji przy użyciu 6-parametrowej transformacji obejmującej obroty wokół 3 osi oraz składowe przesunięcia wzdłuż tych osi, wywołane ruchem płyt tektonicznych. Parametry tej transformacji dla każdej kolejnej realizacji układu ITRF są dostępne w publikacjach podkomisji EUREF. Przejście od układu ETRF89 na epokę obserwacji do układu ETRF89 na epokę 1989.0 wymaga znajomości wektorów V_ETRF składowych prędkości tych stacji w ETRF. Dla stacji europejskich (za wyjątkiem stacji skandynawskich), rejestrowane zmiany ich położenia względem płyty euroazjatyckiej są na poziomie błędów obserwacji; w praktyce przyjmuje się, że są one równe zero. Opis algorytmu wyznaczania pozycji stacji w ETRF89 na epokę 1989.0 wraz z przykładem obliczeniowym podano w pracy (Rogowski i Figurski, 2004).

Układy Borowa Góra i Pułkowo’42

Tradycyjnie stosowanym w pracach geodezyjnych regionalnym systemem odniesienia był tzw. geodezyjny system odniesienia (geodetic datum). Ten statyczny system jest zdefiniowany poprzez elipsoidę obrotową, której oś obrotu jest równoległa do średniej osi obrotu Ziemi. Usytuowanie tej elipsoidy względem figury Ziemi określone jest poprzez jej odstęp od geoidy w punkcie przyłożenia elipsoidy. Początek układu współrzędnych (x¹, x², x³) lub (φ, λ) na elipsoidzie tego systemu (Torge, 1980) pokrywa się ze środkiem geometrycznym elipsoidy, podstawowa oś x³ pokrywa się z osią obrotu elipsoidy, zaś oś x¹ leży w płaszczyźnie południka zerowego (południka Greenwich). Realizacją geodezyjnego systemu odniesienia jest zbiór punktów osnowy geodezyjnej o współrzędnych wyznaczonych w układzie współrzędnych związanym z elipsoidą o ustalonych parametrach geometrycznych (np. duża półoś i spłaszczenie), przyłożoną w odpowiedni sposób do geoidy w wybranym punkcie przyłożenia i zorientowaną względem średniej osi obrotu Ziemi oraz południka zerowego na podstawie obserwacji astronomicznych wykonanych na punktach Laplace’a tej osnowy. Na przestrzeni ostatnich 60 lat w Polsce stosowane były dwa regionalne geodezyjne układy odniesienia:

• „Borowa Góra” oparty na elipsoidzie Bessela z punktem przyłożenia w obecnym Obserwatorium Geodezyjno-Geofizycznym IGiK w Borowej Górze,

• „Pułkowo’42” oparty na elipsoidzie Krasowskiego z punktem przyłożenia w Głównym Obserwatorium Rosyjskiej Akademii Nauk w Pułkowie.

Współrzędne (φ, λ) punktów osnowy geodezyjnej wyrażone w określonym układzie odniesienia stanowią podstawową informację w krajowych zasobach geodezyjnych. Współrzędne płaskie (X, Y) obliczone ze współrzędnych geodezyjnych (φ, λ) przy użyciu określonego odwzorowania mapowego wykorzystywane są bezpośrednio w pracach związanych z wykonywaniem mapy zasadniczej i map urzędowych. Rodzaj odwzorowania i jego parametry określają jednoznacznie wzajemne przyporządkowanie parze liczb (φ, λ) pary liczb (X, Y). W przeszłości układy tak zdefiniowanych współrzędnych płaskich (X, Y) nazywano „państwowym układem”, lub poprawniej „państwowym układem współrzędnych płaskich” (Jarosiński, 1980). Od 2000 r. obowiązują w Polsce dwa układy współrzędnych płaskich:

• 1992 – stosowany w mapach urzędowych o skali 1:10 000 i mniejszych,

• 2000 – stosowany w pracach związanych z wykonywaniem mapy zasadniczej. Oba wymienione układy współrzędnych odniesione są do układu ETRF89 z geocentryczną elipsoidą odniesienia GRS80. Lokalne układy współrzędnych płaskich dowiązywane są do obowiązujących układów współrzędnych płaskich i relacje pomiędzy współrzędnymi w obu układach określane są za pomocą odpowiednich transformacji.

Lokalne systemy astronomiczne (LAS)

Terminologia i formalizm zastosowane do zdefiniowania niebieskich i ziemskich systemów i układów odniesienia mogą być również wykorzystane w definicji systemów obserwacyjnych. Tradycyjne obserwacje geodezyjne oraz obserwacje astronomiczne odniesione są do lokalnych systemów astronomicznych (Local Astronomic System – LAS), z których każdy jest oddzielnym systemem odniesienia (Schwarz i Kryński, 1991; Torge, 2001). LAS jest systemem statycznym zdefiniowanym w trójwymiarowej przestrzeni euklidesowej z użyciem kartezjańskiego układu współrzędnych (x¹, x², x³). Początek P lokalnego systemu astronomicznego odpowiada stanowisku obserwatora. Oś podstawowa x³ układu współrzędnych tego systemu pokrywa się z kierunkiem stycznej do linii pionu w P (kierunek wektora przyspieszenia siły ciężkości) i skierowana jest na zewnątrz Ziemi. Oś ta wyznacza płaszczyznę horyzontu w punkcie P, która jest styczna do powierzchni stałego potencjału siły ciężkości przechodzącej przez P. Oś drugorzędna x¹ określona jest przez prostą powstałą w wyniku przecięcia płaszczyzny horyzontu punktu P z płaszczyzną południka astronomicznego w punkcie P i skierowana jest ku północy. Płaszczyzna południka astronomicznego w punkcie P rozpięta jest na kierunku linii pionu w P (wektor przyspieszenia siły ciężkości) i kierunku przesuniętej równolegle do P średniej osi obrotu Ziemi (kierunek wektora średniej prędkości kątowej Ziemi). Oś trzeciorzędna x², uzupełniająca lewoskrętny system kartezjański, skierowana jest na wschód.

Lokalne układy astronomiczne (LAF)

Praktyczną realizacją lokalnego systemu astronomicznego jest lokalny układ astronomiczny (Local Astronomic Frame – LAF). Początek układu zrealizowany jest poprzez scentrowanie instrumentu na stanowisku P obserwatora. Kierunek osi podstawowej x³ zrealizowany jest poprzez spoziomowanie instrumentu zachowującego jednocześnie wymagane warunki geometryczne. Kierunek osi drugorzędnej x¹ (w płaszczyźnie prostopadłej do osi x³) zrealizowany jest poprzez obserwację kierunku celu o znanym azymucie astronomicznym. Oś trzeciorzędna x², uzupełniająca lewoskrętny system kartezjański, skierowana jest na wschód. W praktyce pomiary na stanowisku P w układzie LAF wykonywane są w układzie współrzędnych sferycznych (A, Z, s), gdzie A jest azymutem astronomicznym, Z – astronomiczną odległością zenitalną, zaś
s – odległością mierzoną wzdłuż linii prostej.

Od LAS do ziemskiego systemu odniesienia

Do zorientowania osi lokalnego systemu astronomicznego wymagana jest znajomość kierunku średniej osi obrotu Ziemi oraz kierunku linii pionu zależnego od lokalizacji punktu P, będącego początkiem systemu. Ze względu na wzajemną nierównoległość linii pionu zmianie punktu początkowego systemu towarzyszy zmiana orientacji osi systemu. Relację pomiędzy systemami LAS o różnych początkach określa się za pośrednictwem relacji pomiędzy każdym LAS i ziemskim systemem odniesienia. Parametrami transformacji LAS do ziemskiego systemu odniesienia są szerokość Φ i długość astronomiczna Λ punktu początkowego P systemu, które określają kierunek linii pionu w P oraz współrzędne P w ziemskim systemie odniesienia. Współrzędne astronomiczne P wyznaczane są z obserwacji astronomicznych lub obliczane jako suma współrzędnych geodezyjnych odniesionych do elipsoidy ziemskiego systemu odniesienia i odpowiednich składowych odchylenia pionu w sensie Helmerta. Współrzędne P w ziemskim systemie odniesienia obliczane są na podstawie współrzędnych geodezyjnych i wysokości tego punktu. Odpowiednie wzory opisujące te relacje można znaleźć w literaturze (np. Schwarz i Kryński, 1991; Czarnecki, 1995).

Podsumowanie

Ćwierć wieku temu Międzynarodowa Unia Astronomiczna IAU oraz Międzynarodowa Unia Geodezji i Geofizyki IUGG zainicjowały działania w kierunku opracowania podstaw teoretycznych definicji systemów odniesienia odpowiadających współczesnym wymaganiom dokładności. W ramach obu unii powołane zostały współpracujące wzajemnie grupy robocze, których działania materializowały się we wprowadzaniu kolejnych udoskonaleń w definicjach systemów odniesienia i realizacji tych systemów.

Systemy odniesienia, układy odniesienia i układy współrzędnych
w astronomii i geodezji

W pierwszym rzędzie wprowadzono nową definicję niebieskiego systemu odniesienia. Miejsce używanych dotychczas naprzemiennie definicji dynamicznych i kinematycznych niebieskich systemów odniesienia IAU zajęła precyzyjna i jednoznaczna kinematyczna definicja niebieskiego systemu odniesienia. Co więcej, wprowadzono zmiany w podstawach teoretycznych definicji tego systemu odniesienia. W miejsce mechaniki newtonowskiej zastosowano mechanikę relatywistyczną. Jednocześnie z uwagi na wysokie wymagania dokładnościowe stawiane nowoczesnej definicji niebieskiego systemu odniesienia uniezależniono ją od precesji. Położenie nowego niebieskiego systemu odniesienia jest kinematycznie ustalone względem systemu inercjalnego, a nie – jak dotychczas – określone na epokę, w odniesieniu do średniego równika i średniej równonocy, jak to miało miejsce w systemach katalogów fundamentalnych, np. FK5 (Kołaczek 2004a; Kryński 2004a).

W istotny sposób zmodernizowano definicję ziemskiego systemu odniesienia. Miejsce statycznego ziemskiego systemu odniesienia zajęły systemy kinematyczne. W wyniku działań zainicjowanych przez IUGG określono podstawy teoretyczne kinematycznego ziemskiego systemu odniesienia oraz stworzono bazę do jego realizacji (Rogowski i Figurski 2004).

Wprowadzanie nowych definicji niebieskiego i ziemskiego systemu odniesienia wymagało dokonania spójnych zmian w definicji pośredniego systemu odniesienia, zmian w opisie relacji pomiędzy systemami odniesienia oraz udoskonalenia definicji systemów czasu.

Z uwagi na potrzebę dokładnej orientacji systemu pośredniego względem systemu niebieskiego udoskonalono modele opisujące precesję i nutację. Model precesji i teoria nutacji opisują ruch podstawowej osi pośredniego systemu odniesienia względem niebieskiego systemu odniesienia. W dotychczasowym modelu precesji i teorii nutacji podstawową osią pośredniego systemu odniesienia była chwilowa oś obrotu Ziemi. Wyniki badań teoretycznych (Guinot, 1979) wykazały, że aby uzyskać wymagane dokładności transformacji systemu niebieskiego do systemu ziemskiego, należy system pośredni odnieść nie do chwilowej osi obrotu Ziemi, lecz do osi, której chwilowe położenie względem niebieskiego systemu odniesienia dawałoby się bardziej precyzyjnie opisać modelem precesyjno-nutacyjnym, a jednocześnie jej ruch w odniesieniu do systemu ziemskiego byłby przewidywalny dokładniej i z większą rozdzielczością czasową (Brzeziński 2004). W ten sposób miejsce chwilowego bieguna określającego kierunek osi podstawowej pośredniego systemu odniesienia zajął początkowo Efemerydalny Biegun Niebieski CEP, a następnie Pośredni Biegun Niebieski CIP – oba bardzo bliskie chwilowemu biegunowi.

Zastąpienie chwilowego bieguna najpierw biegunem CEP, a następnie CIP wiązało się z koniecznością wprowadzenia zasadniczych zmian w definicjach uzupełniających orientację pośredniego systemu odniesienia względem zarówno systemu niebieskiego, jak i ziemskiego. Nowej definicji osi podstawowej systemu pośredniego towarzyszy nowa definicja początku liczenia rektascensji. Miejsce punktu równonocy wiosennej, pełniącego rolę takiego początku, zajął początek efemerydalny systemu niebieskiego CEO, miejsce zaś chwilowego południka Greenwich – początek efemerydalny systemu ziemskiego TEO. Dalszą konsekwencją zmian w definicji systemu pośredniego jest modyfikacja teorii ruchu bieguna – opisującej zmienność położenia systemu pośredniego względem systemu ziemskiego, z zachowaniem spójności ze zmodyfikowanym modelem precesji i teorią nutacji. Zgodnie z nimi IERS wyznacza parametry przeprowadzające odpowiednio system ziemski w system pośredni ziemski oraz system pośredni niebieski w system niebieski (quasi-inercjalny).

Zmianie uległ również parametr transformacji przeprowadzającej system pośredni ziemski w system pośredni niebieski. Tradycyjnie parametrem tym był odniesiony do punktu równonocy wiosennej czas gwiazdowy prawdziwy Greenwich. Zgodnie ze zmodyfikowaną definicją pośredniego systemu odniesienia miejsce czasu gwiazdowego prawdziwego Greenwich (jako parametru opisującego ruch obrotowy Ziemi wokół osi) zajął tzw. Kąt Obrotu Ziemi ERA, określający położenie TEO względem CEO w płaszczyźnie równika systemu pośredniego (Kryński 2004a, 2004b).

Zdefiniowanie niebieskich systemów odniesienia na podstawie uogólnionej teorii względności wiązało się z koniecznością wprowadzenia nowych systemów czasu, tzw. czasu współrzędnych oraz z uściśleniem definicji dotychczas stosowanych systemów czasu, a także relacji pomiędzy tymi systemami (Kryński 2004b).

Udoskonalanie ziemskiego i niebieskiego układu odniesienia, dzięki postępowi w zakresie technik obserwacyjnych oraz postępowi w zakresie modelowania zjawisk geofizycznych zachodzących zarówno w bryle Ziemi, jak i jej otoczeniu (w hydrosferze i atmosferze), umożliwiło podniesienie dokładności wyznaczenia pozycji na powierzchni Ziemi w ciągu ostatniego stulecia o cztery rzędy. Możliwe stało się także utworzenie z dokładnością 1-2 cm kinematycznego układu współrzędnych ziemskich. Powstające kolejne służby monitorujące Ziemię jako planetę i jej zachowanie w przestrzeni pozwolą zapewne w przyszłości na zrealizowanie układu współrzędnych ziemskich z dokładnością o rząd wyższą (Kryński i Rogowski, 2004).

Profesor Jan Kryński był kierownikiem Zakładu Geodezji i Geodynamiki w Instytucie Geodezji i Kartografii w Warszawie

Niniejszą pracę [opublikowaną w wydaniach GEODETY 7-11/2005 – przyp. red] wykonano w ramach badań statutowych IGiK objętych zadaniem „Problemy geodezji i geodynamiki”. Stanowi ona także kontynuację prac prowadzonych w IGiK, rozpoczętych w trakcie opracowywania „Rocznika Astronomicznego” na 2004 rok.

Słowniczek skrótów

BCRS (Barycentric Celestial Reference System) – Barycentryczny Niebieski System Odniesienia

BIH (Bureau International de l’Heure) – Międzynarodowe Biuro Czasu

BIPM (Bureau International des Poids et Mesures) – Międzynarodowe Biuro Wag i Miar w Paryżu

CEO (Celestial Ephemeris Origin) – Niebieski Efemerydalny Punkt Początkowy

CEP (Celestial Ephemeris Pole) – Efemerydalny Biegun Niebieski

CIO (Conventional International Origin) – międzynarodowy konwencjonalny (umowny) średni biegun północny Ziemi

CIP (Celestial Intermediate Pole) – Pośredni Biegun Niebieski

CRP (Conventional Reference Pole) – Konwencjonalny (Umowny) Biegun Odniesienia

CTRS (Conventional Terrestrial Reference System) – Konwencjonalny (Umowny) Ziemski System Odniesienia

CTS (Conventional Terrestrial System) – Umowny (Konwencjonalny) System Ziemski

EOP (Earth Orientation Parameters) – parametry ruchu obrotowego Ziemi

EPN (EUREF Permanent GPS Network) – sieć EUREF permanentnych stacji GPS

ERA (Earth Rotation Angle) – Kąt Obrotu Ziemi

ET (Ephemeris Time) – Czas Efemeryd

ETRF89 (European Terrestrial Reference Frame 89) – Europejski Ziemski Układ Odniesienia 89

ETRS89 (European Terrestrial Reference System 89) – Europejski Ziemski System Odniesienia 89

EUREF-POL92 – sieć 11 stacji na terenie Polski dowiązanych do układu ETRF89

GCRS (Geocentric Celestial Reference System) – Geocentryczny Niebieski System Odniesienia

GMST (Greenwich Mean Sidereal Time) – średni czas gwiazdowy Greenwich

GPST (GPS Time) – czas GPS

GRS67 (Geodetic Reference System 1967) – Geodezyjny System Odniesienia 1967

GRS80 (Geodetic Reference System 1980) – Geodezyjny System Odniesienia 1980

GST (Greenwich Sidereal Time) – prawdziwy czas gwiazdowy Greenwich

IAG (International Association of Geodesy) – Międzynarodowa Asocjacja Geodezji

IAU (International Astronomical Union) – Międzynarodowa Unia Astronomiczna

ICRF (International Celestial Reference Frame) – Międzynarodowy Niebieski Układ Odniesienia

ICRS (International Celestial Reference System) – Międzynarodowy Niebieski System Odniesienia

IERS (International Earth Rotation and Reference Systems Service) – Międzynarodowa Służba Ruchu Obrotowego Ziemi i Systemów Odniesienia Międzynarodowej Asocjacji Geodezji

IGS (International GNSS Service) – Międzynarodowa Służba GNSS

IPMS (International Polar Motion Service) – Międzynarodowa Służba Ruchu Bieguna

IRS, IRS_NIEBIESKI^,IRS_ZIEMSKI (Intermediate Reference System) – Pośredni System Odniesienia

ITRF (International Terrestrial Reference Frame) – Międzynarodowy Ziemski Układ Odniesienia

ITRS (International Terrestrial Reference System) – Międzynarodowy Ziemski System Odniesienia

IUGG (International Union of Geodesy and Geophysics) – Międzynarodowa Unia Geodezji i Geofizyki

LAF (Local Astronomic Frame) – lokalny układ astronomiczny

LAS (Local Astronomic System) – lokalny system astronomiczny

NRO (Non-Rotating Origin) – Nieobracający się Punkt Początkowy

POLREF – 360 stacji sieci zagęszczającej punkty EUREF-POL92 (w układzie ETRF89)

TAI (International Atomic Time, Le temps atomique international) – Międzynarodowy Czas Atomowy

TCB (Barycentric Coordinate Time) – czas współrzędnych barycentrycznych

TCG (Geocentric Coordinate Time) – czas współrzędnych geocentrycznych

TDB (Barycentric Dynamical Time) – Barycentryczny Czas Dynamiczny

TEO (Terrestrial Ephemeris Origin) – Ziemski Efemerydalny Punkt Początkowy

TT (Terrestrial Time) – Czas Ziemski

UT (Universal Time) – czas uniwersalny

UT1 (Mean Universal Time) – czas uniwersalny średni

UTC (Universal Time Coordinated) – Czas Uniwersalny Koordynowany

WGS72 (World Geodetic System 1972) – Światowy System Geodezyjny 1972

WGS72 (World Geodetic System 1972) – Światowy System Geodezyjny 1980

ZT (Zonal Time) – czas strefowy

Bibliografia

Argus D.F., Gordon R.G., 1991, No-Net-Rotation Model of Current Plate Velocities Incorporating Plate Motion Model Nuvel-1, „Geophysical Research Letters”, Vol. 18; lAudoin C., Guinot B., Gordon R.G., 2001, The Measurement of Time, Time, Frequency and the Atomic Clock, Cambridge University Press, Cambrigde, UK; lBoucher C., 1994, Specifications for Reference Frame Fixing in the Analysis of a EUREF GPS Campaign, Report on the Symposium of the IAG Subcommission for Europe (EUREF) held in Warsaw, Poland, 8-11 June 1994, EUREF Publication No 3, „Astronomisch-Geodätische Arbeiten”, Heft Nr 54, München; lBrzeziński A., 2004, Nowy model precesyjno-nutacyjny, Nowe obowiązujące niebieskie i ziemskie systemy i układy odniesienia oraz ich wzajemne relacje, red. J. Kryński, Seria Monograficzna Nr 10, IGiK, Warszawa; lCapitaine N., 2000, Definition of the Celestial Ephemeris Pole and the Celestial Ephemeris Origin, Towards Models and Constants for Sub-Microarcsecond Astrometry, (eds.) K.J. Johnston, D.D. McCarthy, B.Luzum, G. Kaplan, UNSO; lCapitaine N., Guinot B., Souchay J., 1986, A Non-Rotating Origin on the Instantaneous Equator: definition, properties and use, „Celestial Mechanics”, Vol. 39; lCapitaine N., Guinot B., 1988, A Non-Rotating Origin on the Instantaneous Equator, A.K. Babcock and G.A. Wilkins (eds.), „The Earth’s Rotation and Reference Frames for Geodesy and Geophysics”; lCapitaine N., Guinot B., McCarthy D.D., 2000, Definition of the Celestial Ephemeris Origin and of UT1 in the International Celestial Reference Frame, „Astronomy and Astrophysics”, Vol. 355; lCapitaine N., Wallace P.T., McCarthy D.D., 2003, Expressions to implement the IAU 2000 definition of UT1, „Astronomy and Astrophysics”, Vol. 406; lCzarnecki K, 1995, Geodezja współczesna w zarysie, Wydawnictwo Wiedza i Życie; lDehant V. i in., 1999, Considerations concerning the non-rigid Earth nutation theory, „Celestial Mechanics”, Vol. 72; lFricke W., 1985, Fundamental Catalogues, Past, Present and Future, „Celestial Mechanics”, Vol. 36, D. Reidel Publishing Company; lFricke W., Kopff A., 1963, Fourth Fundamental Catalogue (FK4), „Veröffentlichungen Astronomisches Rechen-Institut Heidelberg”, No 10, Verlag G. Braun, Karlsruhe; lFricke W., Schwan H., Lederle T., 1988, Fifth Fundamental Catalogue (FK5). Part I. The Basic Fundamental Stars, „Veröffentlichungen Astronomisches Rechen-Institut Heidelberg”, No 32, Verlag G. Braun, Karlsruhe; lGuinot B., 1979, Basic Problems in the Kinematics of the Rotation of the Earth, in D.D. McCarthy and J.D. Pilkington (eds), „Time and the Earth’s Rotation”, D. Reidel Publ.; lIAG, 1971, Geodetic Reference System 1967, Publ. Spéc. No 3 du „Bulletin Géodésique”, Paris; lIAG, 1980, The Geodesist’s Handbook 1980, „Bulletin Géodésique”, Vol. 54, No 3, Paris; lIAG, 1992, The Geodesist’s Handbook 1992, „Bulletin Géodésique”, Vol. 66, No 2, Springer, International; lIAU, 1996, Transactions of the International Astronomical Union, XXIIB, (ed.) I. Appenzeller, Dodrecht, Kluwer, The Netherlads;

IAU, 1999, Transactions of the International Astronomical Union, XXIIIB, (ed.) J. Andersen, Dodrecht, Kluwer, The Netherlads; lIAU, 2001, Transactions of the International Astronomical Union, XXIVB, (ed.) H. Rickman, Dodrecht, Kluwer, The Netherlads; lIERS, 2003, IERS Conventions (2003), IERS Technical Note 32, (ed.) D.D. McCarthy, G. Petit, November 2003, Observatoire de Paris, Paris. lJarosiński E., 1980, Osnowy geodezyjne, „Służba Geodezyjna i Kartograficzna GUGiK 1945-1980”, Biuletyn Informacyjny, Tom XXIV, Numer Specjalny 1-2/1980, GUGiK – IGiK, PPWK, Warszawa; lKołaczek B., 1989, Observational Determination of the Earth’s Rotation, „Gravity and Low-Frequency Geodynamics”, (ed.) R. Teisseyre, PWN Warszawa, Elsevier Amsterdam–Oxford–New York–Tokyo; lKołaczek B., 2004, Niebieskie fundamentalne systemy odniesienia i ich realizacje, „Nowe... [patrz Brzeziński A., 2004]; lKovalevsky J., 2002, Comparison of “Old” and “New” Concepts: Reference Systems, „Proceedings of the IERS Workshop on the Implementation of the New IAU Resolutions”, IERS Technical Note No 29, Observatoire de Paris; lKryński J., 2004a, Relacje pomiędzy systemami niebieskimi i systemem ziemskim, „Nowe obowiązujące... [patrz Brzeziński A., 2004];

Kryński J., 2004b, Nowe skale czasu i idea pośredniego systemu odniesienia, „Nowe obowiązujące... [patrz Brzeziński A., 2004]; lKryński J. (ed.), 2004c, „Nowe obowiązujące... [patrz Brzeziński A., 2004]; lKryński J., Rogowski J.B., 2004, Systemy i układy odniesienia w geodezji, geodynamice i astronomii, Nowe obowiązujące... [patrz Brzeziński A., 2004]; lKryński J., Sękowski M., 2002, Rocznik Astronomiczny na rok 2003, IGiK, Warszawa, ed. J. Kryński; lKryński J., Sękowski M., 2003, Rocznik Astronomiczny na rok 2004, IGiK, Warszawa, ed. J. Kryński; lKryński J., Sękowski M., 2004, Rocznik Astronomiczny na rok 2005, IGiK Warszawa, ed. J. Kryński; lLandau L.D., Lifszyc E.M., 1980, Teoria pola, PWN, Wydanie III, Warszawa; lLieske J.H., Lederle T., Fricke W., Morando B., 1977, Expression for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants, „Astronomy and Astrophysics”, Vol. 304; lMcCarthy D.D., Capitaine N., 2002, Compatibility with Past Observations, „Proceedings… [patrz Kovalevsky J., 2002]; lMinster J.B., Jordan T.H., 1978, Present-day plate motions, „Journal of Geophysical Research”, Vol. 83; lMoritz H., 1984, Geodetic Reference System 1980, The Geodesist’s Handbook 1984, „Bulletin Géodésique”, Vol. 58, No 3; lPerryman M.A.C., Lindegren L., Kovalevsky J. i inni, 1997, The Hipparcos Catalogue, Letter to the Editor, „Astronomy and Astrophysics”, Vol. 323; lPetit G., (2002): Comparison of “Old” and “New” Concepts: Coordinate Times and Time Transformations, Proceedings… [patrz Kovalevsky J., 2002,]; lRogowski J.B., Figurski M., 2004, Ziemskie globalne systemy odniesienia i ich realizacje, „Nowe... [patrz Brzeziński A., 2004]; lSchutz B.F., 2002, Wstęp do ogólnej teorii względności, Wydawnictwo Naukowe PWN, Warszawa, 2002; lSchwarz K.P., Kryński J., 1991, Fundamentals of Geodesy, UCSE Report No. 10007, Department of Surveying Engineering, The University of Calgary, Alberta, Canada; lSeidelmann P.K., 1982, 1980 IAU Theory of Nutation, the Final Report of the IAU Working Group for Nutation, „Celestial Mechanics”, Vol. 27; lTorge W., 1980, Geodesy, Walter de Gruyter, Berlin-New York; lTrajdos-Wróbel T., 1966, Matematyka dla inżynierów, WNT, Warszawa; lWahr J.M., 1981, The Forced Nutations of an Elliptical, Rotating, Elastic and Oceanless Earth, Geophys. J., Roy. Astron. Soc., 64.

Opracowanie zamieszczono na Geoforum w styczniu 2006 r.