|
Roman Kadaj
Poznaliśmy już wzory i aplikacje podstawowych odwzorowań: Gaussa-Krügera i quasi-stereograficznego. Kawał roboty za nami, ale do kompletu przeliczeń współrzędnych brakuje jeszcze reguł przechodzenia pomiędzy elipsoidami WGS-84 i Krasowskiego, czy – precyzyjniej – pomiędzy systemami ETRF ’89 i Pułkowo ’42. Matematycznie rzecz ujmując, chodzi o parametry transformacji przestrzennej pomiędzy układami elipsoidalnymi (podstawą do ich określenia powinny być punkty osnów geodezyjnych wyznaczonych ongiś w systemie Pułkowo ’42 oraz obecnie w systemie ETRF-89). Zacznijmy więc od podstaw.
Współrzędne zamiast adresu pocztowego
Pozycja dowolnego punktu na powierzchni Ziemi jest określana jednoznacznie na przykład za pomocą współrzędnych geodezyjnych (B, L, H) lub kartezjańskich geocentrycznych (X, Y, Z) w umownym systemie elipsoidalnym (rys. 1.). Te dwa rodzaje współrzędnych traktujemy jako informacje równoważne, ponieważ przejście (przeliczenie) pomiędzy nimi (B, L, H) ó (X, Y, Z) dokonuje się poprzez ścisłe, wzajemnie jednoznaczne formuły matematyczne. Tak więc można powiedzieć, że współrzędne (B, L, H) lub (X, Y, Z) określają równoważnie pozycję lub pełnią funkcję „adresu” punktu (także w znaczeniu dosłownym, o czym można się przekonać oglądając wizytówki niektórych firm geodezyjnych).
Rys. 1. Współrzędne geodezyjne i kartezjańskie centryczne
Współrzędne B, L określają pozycję „poziomą” (rzut punktu na powierzchnię elipsoidy), natomiast wysokość elipsoidalna H uzupełnia te dane do pełnej trójwymiarowej informacji przestrzennej. Należy w tym miejscu dodać, że sama wysokość elipsoidalna (geometryczna) nie zastąpi jednak potrzebnych w praktyce wysokości niwelacyjnych (normalnych, czy może quasi-ortometrycznych) w przyjętym systemie wysokości, względem naturalnej powierzchni poziomej (geoidy), a raczej jej praktycznej generalizacji (quasi-geoidy). Z drugiej strony, same wysokości niwelacyjne, bez dołączonego modelu geoidy (quasi-geoidy) względem elipsoidy, nie dają pełnej informacji przestrzennej (geometrycznej) o położeniu punktu. Przekonamy się więc w różnych zadaniach geodezyjnych, że kompletna informacja wysokościowa powinna zawierać dane pozwalające na odtworzenie zarówno wysokości geometrycznej (elipsoidalnej), jak też wysokości niwelacyjnej punktu w przyjętym systemie wysokości. Należy podkreślić, że wiele aktualnych zadań geodezyjnych (w tym transformacje pomiędzy różnymi systemami elipsoidalnymi, tworzenie sieci GPS) ma w pełni charakter trójwymiarowy, w odróżnieniu od zadań klasycznych lub o charakterze lokalnym, sprowadzających się do metod geodezji płaskiej (dwuwymiarowej) lub tzw. płasko-wysokościowej (oddzielnie płaskiej i wysokościowej).
Przeliczamy: [B, L, H] na [X, Y, Z]...
Niech punkt P ma współrzędne geodezyjne (B, L, H). Formuły przeliczenia ich na współrzędne kartezjańskie (X, Y, Z) wywodzą się z ogólnych zależności:
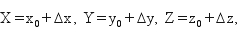 (1)
gdzie x0, y0, z0 oznaczają współrzędne rzutu normalnego P0 punktu P na powierzchnię elipsoidy, zaś Δx, Δy, Δz – składowe wektora P0P o długości H (powinien być spełniony warunek H2 = Δx2 + Δy2 + Δz2).
Szukane związki ze współrzędnymi B, L, H (rys. 2) są następujące:
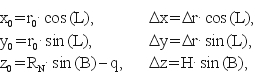 (2)
gdzie:
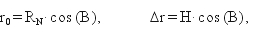 (2a)
RN jest długością odcinka normalnej, mierzoną od punktu P0 do punktu S przecięcia z osią obrotu elipsoidy – jest to zarazem promień krzywizny przekroju poprzecznego (pierwszego wertykału) elipsoidy w punkcie P0 (dla szerokości B), wyrażający się wzorem:
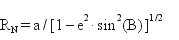 (3)
(przypomnijmy, że użyliśmy go już w poprzednim wykładzie obok promienia krzywizny przekroju południkowego RM oraz średniego promienia krzywizny; e – mimośród, e2 = (a2 - b2) / a2; a, b – półosie elipsoidy). Parametr q (rys. 2) jako ujemna współrzędna punktu S wyraża się wzorem:
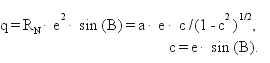 (4)
Składając wzory (1), (2) i (3) otrzymujemy formuły:
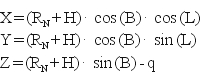 (5)
(wielkości RN i q są również funkcjami szerokości B).
Rys. 2. Elementy przekroju południkowego i rzutu poziomego
... lub odwrotnie [X, Y, Z] na [B, L, H]
Aby dokonać przeliczenia odwrotnego należałoby odwrócić zależności (5), wyznaczając z nich B, L i H na podstawie X, Y, Z. Mając na uwadze to, że w definicji promienia RN oraz wielkości q kryje się również szerokość B, odwrócenie (5) nie jawi się jako równie proste zadanie (można je sprowadzić do rozwiązania równania algebraicznego stopnia wyższego od 2). Dlatego posługujemy się chętnie metodami kolejnych przybliżeń. Jedna z prostych metod polega na wykorzystaniu następującej zależności, którą można otrzymać z (5) lub wprost z rysunku 2 (zob. np. [10]* ):
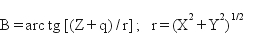 (6)
(r – odległość punktu P od osi obrotu elipsoidy), przy czym określona wyżej wzorem (4) „względnie mała” wielkość q jest (niestety) istotną funkcją B, dlatego zapis (6) nie oznacza jeszcze jawnego rozwiązania. Formułę (6) można jednak użyć do tworzenia kolejnych przybliżeń B0, B1, B2, ... niewiadomej B (stosownie do tego parametr q jako funkcja B przyjmuje wartości kolejnych przybliżeń q0, q1, q2, ...).
Algorytm: [X, Y, Z] na B
Krok 0: przyjmujemy q = q0 = 0 i obliczamy B według wzoru (6), notując je jako B0 (przybliżenie początkowe);
Krok 1: obliczamy przybliżoną wartość q1 zgodnie z wzorem (4) jako funkcję B0, a następnie nowe przybliżenie B1 szerokości B według wzoru (6);
Krok 2: obliczamy przybliżenie q2 zgodnie z wzorem (4) jako funkcję B = B1, a następnie aktualne przybliżenie B2 szerokości B według wzoru (6);
... itd.
Proces zatrzymujemy, jeśli różnica kolejnych przybliżeń jest mniejsza niż założony dopuszczalny błąd numeryczny wyznaczenia B. Zwykle konieczną dokładność otrzymuje się po kilku krokach.
Obliczenie brakujących współrzędnych L, H nie przedstawia już trudności:
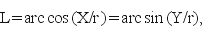 (7)
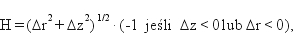 (8)
przy czym przyrosty Dr, Dz obliczamy ze wzorów:
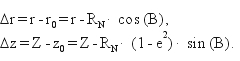 (9)
Współrzędne B, L wyrażone w radianach przeliczamy ostatecznie do miary stopniowej.
Przechodzimy pomiędzy elipsoidami
Przypuśćmy, że punkt P ma współrzędne [X, Y, Z]K w centrycznym układzie kartezjańskim elipsoidy Krasowskiego. Pytamy, jakie będą analogiczne współrzędne [X, Y, Z]G tego punktu w układzie elipsoidy GRS-80 (WGS-84) (rys. 3). Możemy oczywiście formułować również zadanie odwrotne (zgodnie z ogólnym schematem przeliczeń współrzędnych sformułowanych w pierwszym wykładzie).
Rys. 3. Układy kartezjańskie elipsoid
Jak już wspominaliśmy w pierwszym wykładzie, przeliczenie takie jest problemem transformacji przestrzennej (trójwymiarowej) układów współrzędnych związanych z różnymi elipsoidami odniesienia. Dla wykonania konkretnych zadań praktycznych parametry takiej transformacji muszą być oczywiście znane. Na takie okoliczności wyznaczono je w GUGiK na podstawie punktów sieci POLREF (dysponowano współrzędnymi kartezjańskimi punktów w obu układach elipsoidalnych dzięki zbiorom danych archiwalnych w systemie Pułkowo ’42 oraz nowym pomiarom w systemie ETRF ’89). Nie będziemy wnikać w sam proces estymacji tych parametrów. Ograniczymy się jedynie do podania finalnych formuł praktycznych i ich charakterystyk dokładnościowych. Najbardziej ogólna formuła liniowej transformacji przestrzennej wyraża się następującymi wzorami (użyjemy znaczników K i G dla odróżnienia konkretnie stosowanych elipsoid: Krasowskiego i GRS-80 (WGS-84)):
Transformacja [X,Y,Z]G na [X,Y,Z]K
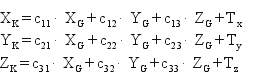
lub w bardziej eleganckiej postaci macierzowej: XK = C U XG + T, gdzie T jest wektorem przesunięcia środków układów określonym w układzie elipsoidy Krasowskiego; C – macierzą współczynników (parametrów) cij (i, j:=1, 2, 3). Aby powyższa transformacja zachowywała kształty (konforemność) figur (co w naszym zadaniu jest wymogiem podstawowym), macierz C musi mieć cechę ortogonalności. Myślę, że nie zgrzeszymy nadmiarem teorii, jeśli dodamy, że dla macierzy ortogonalnej zachodzi związek:
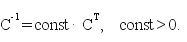 (11)
Jeśli oznaczymy const = 1/m2, to liczba m będzie skalą podobieństwa dla transformacji (10).
W naszym konkretnym zastosowaniu przyjmuje się dodatkowe uproszczenie formuły (10), wynikające stąd, że układy kartezjańskie rozważanych elipsoid mają osie zbliżone do równoległych (odchylenia od równoległości nie przekraczają 1”). Uproszczenie to polega na przyjęciu następujących podstawień:
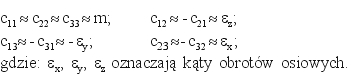 (12)
Zgodnie z najnowszym projektem instrukcji technicznej G-2 [13], ostatecznie uzgodnione parametry transformacji, z uwzględnieniem uproszczeń w postaci (12), są następujące (dane te zostały przekazane przez GUGiK do wiadomości Europejskiej Podkomisji IAG: CERCO, WG VIII):
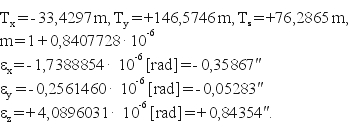 (13)
Bez określonych uproszczeń (12) elementy ortogonalnej macierzy C są następujące (według Wytycznych Technicznych G-1.10 [6]):
 (14)
Interesującym spostrzeżeniem może być to, że przy przejściu z elipsoidy GRS-80 (WGS-84) na elipsoidę Krasowskiego (jako elipsoidę lokalną) następuje dodatnia zmiana skali wynosząca ok. 0,84 mm/km. Można powiedzieć, że jest to obecnie identyfikowane odchylenie pomiędzy współczesnym „metrem satelitarnym”, a „metrem klasycznym” (dłuższym) wynikającym w istocie z realizacji skali osnów podstawowych. Wielkość ta, jako praktycznie bardzo mała, świadczy raczej o wysokiej precyzji pomiarów klasycznych, gdzie jak wiadomo, skala sieci była określana przez bardzo pracochłonne pomiary liniowe baz triangulacyjnych. Przy tej okoliczności oddajmy więc należny hołd i słowa uznania dawnym pokoleniom geodetów za dobrze wykonaną robotę.
Transformacja odwrotna: [X, Y, Z]K Þ [X, Y, Z]G
Odwrócenie zależności (10) prowadzi do formuł ogólnych:
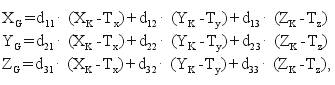 (15)
gdzie współczynniki d są elementami macierzy D, która jest po prostu macierzą odwrotną do C. Elementy te wyznaczamy natychmiast, kierując się własnością (11). Otrzymują one następujące wartości:
 (16)
Stosując własność (11), możemy również odwrócić formułę (10) przy założeniu uproszczeń zawartych w związkach (12) i parametrach (13). Analiza dokładności numerycznej potwierdza, że uproszczenia w tej postaci są w pełni wystarczające dla całego obszaru Polski („resztowa” nieortogonalność nie jest praktycznie istotna).
Przykłady do testowania Bierzemy 5 punktów (rys. 4) i zadajemy ich współrzędne B, L, H w układzie GRS-80 (WGS-84).
Rys. 4. Szkic punktów testowych
Zgodnie z przyjętymi zasadami dokonujemy przekształceń:
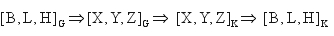 (17)
(Wyniki obliczeń przedstawia tabela 1.)
Powyższy przykład ilustruje geometrię wzajemnego układu elipsoid w obszarze Polski: Różnice pomiędzy wysokościami elipsoidalnymi HG ? HK są lokalnymi odstępami elipsoid.
Jak widać, w „środkowym” punkcie obszaru Polski odstęp ten wynosi ok. 34,3 m. Zauważamy ponadto, że współrzędne geodezyjne B, L na elipsoidzie Krasowskiego są większe średnio o ok. 1” w szerokości B i ok. 6,5” w długości L. Dokładność zapisu współrzędnych geodezyjnych B, L zależy od wymaganej dokładności zapisu odpowiadających współrzędnych płaskich (w odwzorowaniu): Dokładność do 0,0001” gwarantuje, że odpowiadający błąd zaokrąglenia współrzędnych płaskich nie przekracza 0,003 m (zmiana szerokości geodezyjnej B o 1” odpowiada przyrostowi łuku południka o ok. 30 m, zaś zmiana długości L o 1” daje przyrost długości łuku równoleżnika ok. 20 m).
Skąd brać wysokości elipsoidalne?
Jak pamiętamy z pierwszego wykładu, aby przeliczyć współrzędne płaskie układu odwzorowawczego jednej elipsoidy na współrzędne płaskie układu odwzorowawczego drugiej elipsoidy, powinniśmy przejść ścieżką poprzez współrzędne elipsoidalne, zgodnie z formułą (17) lub odwrotną (zależnie od konkretnych układów). W tym celu trzeba przyjąć przybliżone wysokości elipsoidalne punktów w systemie, z którego wychodzimy. Przypuśćmy, że przeliczamy współrzędne z układu „1992” do układu „1965”. Po drodze realizujemy przeliczenie według schematu (17). Zatem powinniśmy dysponować informacjami o wysokościach elipsoidalnych GRS-80 (oznaczonych przez HG). Przy przeliczaniu odwrotnym będzie natomiast obowiązywać schemat odwrotny do (17) i wtedy należy przyjąć wysokości elipsoidalne Krasowskiego (oznaczone HK). Ponieważ jednak (jak pamiętamy z pierwszego wykładu) przy przeliczaniu współrzędnych płaskich wymienione wysokości mają tylko niewielki wpływ na zmiany współrzędnych płaskich, wystarczy posłużyć się wartościami orientacyjnymi tych wysokości (zaokrąglonymi do metrów, a nawet do dziesiątek metrów). W tym celu możemy wykorzystać stosowane w praktyce wysokości normalne Hn (np. pozyskane z interpolacji na mapie). Wykorzystując fakt, że elipsoida Krasowskiego generalizuje w pewnym sensie przebieg quasi-geoidy (maksymalne odchylenia w obszarze Polski są rzędu kilku metrów), zaś przeciętny odstęp elipsoid (jak wynika z tabeli 1) wynosi ok. 34 m, z wystarczającą dla naszego celu dokładnością możemy przyjąć (rys. 5):
Rys. 5. Wysokości elipsoidalne i normalne
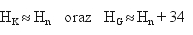 (18)
Warto w tym miejscu dodać, że współcześnie wyznaczane ? przy wykorzystaniu techniki GPS – punkty osnów geodezyjnych, w wyniku bezpośredniego wyrównania sieci wektorów w układzie elipsoidy GRS-80 (WGS-84) mają określone wysokości elipsoidalne HG. Mogą być one przeliczone na wysokości niwelacyjne przy wykorzystaniu numerycznego modelu geoidy (quasi-geoidy) lub poprzez lokalną interpolację odstępów geoidy od elipsoidy na podstawie punktów dostosowania wyznaczonych drogą niwelacji geometrycznej.
Przeliczenia „na skróty”
Elementarne przekształcenia składające się na schemat (17) można numerycznie poskładać, dochodząc do wzorów realizujących bezpośrednie przeliczenia:
Względna „bliskość” parametrów różnych elipsoid odniesienia skłania do tworzenia alternatywnych formuł różnicowych. Sprowadzają się one do określenia przyrostów współrzędnych geodezyjnych, a w naszym przypadku
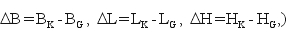 (19)
w funkcji współrzędnych B, L, H jednej z elipsoid. Znajomość odpowiednich różnic pozwala oczywiście dokonać stosownego przeliczenia współrzędnych.
Przeliczenie [ B, L, H ]G => [ B, L, H ]K
Załóżmy, że dane są współrzędne geodezyjne B, L oraz wysokość elipsoidalna H punktu w układzie elipsoidy GRS-80. Szukamy analogicznych współrzędnych geodezyjnych B,L na elipsoidzie Krasowskiego (by potem przeliczyć je np. do układu „1965”). Potrzebne przyrosty DB, DL, DH wyznaczymy, stosując następujące formuły wielomianowe:
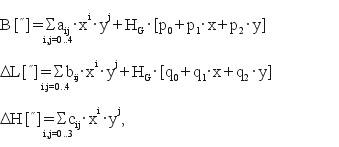 (20)
gdzie: x = (BG” – 187200,0000”) · 0,45 · 10-4, y = (LG” – 68400,0000”) · 0,45 · 10-4 , HG – wysokość elipsoidalna GRS-80 w metrach (scentrowane i unormowane argumenty, przy czym dane współrzędne geodezyjne są wyrażone w sekundach stopniowych, stałe centrujące odpowiadają punktowi o współrzędnych B0 = 52o , L0 = 52o , liczba 0,45 · 10-4 jest faktorem normującym, tak że w obszarze Polski będzie z pewnością: | x | < 1 i | y | < 1 ), aij, bij (i,j = 0, 1, 2, 3, 4), pi, qi (i = 0, 1, 2), cij (i,j = 0, 1, 2, 3) – stałe parametry, których wartości podano w tabeli 2.
Przeliczenie odwrotne: [ B, L, H ]K => [ B, L, H ]G
Używane tu różnice DB, DL, DH powinny być identyczne z różnicami wyznaczonymi według wzorów (20). Teraz nie dysponujemy jednak potrzebnymi argumentami BG, LG, HG lecz BK, LK, HK. Zatem pewnej niewielkiej zmianie ulegną wartości współczynników aij i bij – podano je w drugiej kolumnie tabeli 2.
Nie trzeba natomiast korygować wartosci parametrów cij oraz pi i qi . W ogólnych wzorach (20) w miejsce HG wstawiamy HK + DH, gdzie pierwszy składnik jest dany, zaś drugi obliczony. Zmianie podlega też sposób obliczania argumentów x i y. Dla porządku podajemy wzory w formie adekwatnej do transformacji odwrotnej:
 (21)
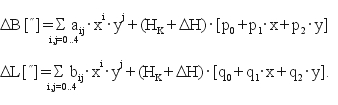 (21a)
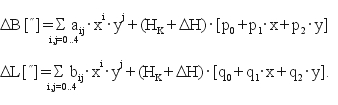 (21b)
Roman Kadaj jest profesorem nauk technicznych, kierował Katedrą Geodezji na Akademii Rolniczej w Krakowie
Opracowanie 2006
* Spis literatury znajduje się w części ostatniej pt. „Osnowy
|  nadchodzące wydarzenia
nadchodzące wydarzenia
 zobacz pozostałe
zobacz pozostałe