|
Roman Kadaj
Krótka synteza
Stosowane układy kartograficzne podzieliliśmy w zależności od tego z jakiej elipsoidy i systemu odniesienia się wywodzą, a także od rodzaju zastosowanego odwzorowania. Ujmuje to syntetycznie tabela 1.
Tab. 1. Klasyfikacja układów kartograficznych
Pamiętamy ponadto, że:
n przy przeliczaniu współrzędnych pomiędzy układami odwzorowawczymi różnych elipsoid przechodzimy (w zasadzie) ścieżką przez współrzędne elipsoidalne obu systemów. Wiąże się to z uwzględnieniem przynajmniej przybliżonej informacji o wysokości elipsoidalnej punktu. Przykładowo, przechodząc z układu „1965” do układu „1992” stosujemy schemat przeliczeń:
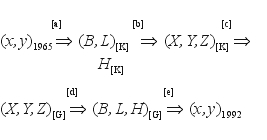 (1) jakkolwiek operacje oznaczone [b], [c], [d] można poskładać zastępując ją jednym przekształceniem (B,L,H)[K] na (B,L,H)[G] (znacznik [K] oznacza elipsoidę Krasowskiego, zaś [G] – elipsoidę GRS-80). Bezpośrednie przeliczenie (x, y)1965 na (x, y)1992 lub także (B, L)[K] na (B, L)[G] jest możliwe przy zaniedbaniu wpływu wysokości.
n Aby przeliczyć współrzędne pomiędzy układami (lub strefami układu) tej samej elipsoidy
nie potrzeba „podpierać się” informacją wysokościową; stosujemy dwa sposoby: Sposób podstawowy oznacza pośrednie przejście na współrzędne geodezyjne B, L:
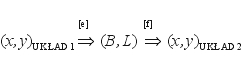 (2)
(oznaczenia: UKŁAD 1, UKŁAD 2 zastępują nazwy pewnych układów lub stref układów). Drugi sposób polega na zastosowaniu bezpośredniego przekształcenia wiernokątnego:
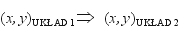 (3)
Ten wykład poświęcimy algorytmom podstawowych odwzorowań i ich aplikacjom do państwowych układów współrzędnych. Jak widać z tabeli 1, będą to odwzorowania: Gaussa-Krügera oraz quasi-stereograficzne, przy czym jak poucza teoria por. Panasiuk, Balcerzak, Gdowski [9]*, odwzorowanie quasi-stereograficzne tworzy się łatwo z odwzorowania Gaussa-Krügera. Należy zatem stwierdzić, że odwzorowanie Gaussa-Krügera stanowić będzie istotny element proceduralny w tworzeniu ścieżek przekształceń. Na początku zapoznamy się z pewnym uniwersalnym „narzędziem” do praktycznej realizacji odwzorowań konforemnych. Ze względu na konieczne ograniczenie ram tej publikacji Czytelnik wybaczy, że pomijane są wszelkie wyprowadzenia i dowody. Więcej informacji znajdzie się w publikowanych już wkrótce Wytycznych Technicznych G-1.10 [6]. Formuły odwzorowawcze i parametry układów współrzędnych [6].
„Kurczenie lub rozciąganie i skręcanie”
Inne ważne pojęcie to elementarna skala liniowa (m) lub parametr pochodny – elementarne zniekształcenie długości s = m-1 (mnożąc np. przez 105 wyrażamy je w cm/km). Niech będzie dany na elipsoidzie punkt P o współrzędnych (B, L) oraz w bliskim „różniczkowym” jego otoczeniu drugi punkt Q odległy o ds. Punkty te odwzorują się na płaszczyźnie w odpowiednie punkty P’ oraz Q’, zaś łuk PQ o długości ds w odpowiadający łuk P’Q’ o długości dS. Elementarną skalę liniową definiujemy stosunkiem m = dS/ds. W odwzorowaniach wiernokątnych jest ona niezależna od azymutu łuku PQ i wyraża się funkcją położenia np. we współrzędnych geodezyjnych (B,L) lub odwzorowawczych (x, y). Konwergencja (zbieżności południków) γ mierzy natomiast różnicę pomiędzy azymutem łuku PQ (na elipsoidzie) a azymutem topograficzznym (kątem kierunkowym) łuku P’Q’ w układzie współrzędnych x,y (na płaszczyźnie odwzorowawczej).
Analogiczne definicje, ale w znaczeniu relatywnym odnosić się będą do wiernokątnego przekształcenia jednej płaszczyzny odwzorowawczej (Ω1) w inną (Ω2), zgodnie warunkiem (5). Przypuśćmy, że odcinek elementarny PQ o długości ds jest równoległy do osi x na płaszczyźnie Ω1, zaś po przekształceniu przyjmuje on na drugiej płaszczyźnie położenie P’Q’ (rys. 2)
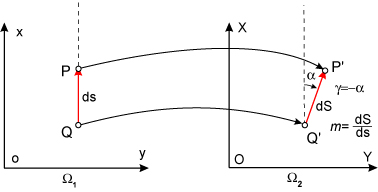
o kącie kierunkowym ai długość dS. Stosunek dS/ds wyznacza skalę elementarną przekształcenia (mierzącą lokalną „rozciągliwość” lub „kurczliwość” pola) zaś wartość ujemna kąta a określa konwergencję jako lokalne skręcenie obrazu γ= -a. Para wielkości (m , g) zmieniających się w obszarze odwzorowania definiuje pole (wektorowe)zniekształceń.
Weźmy teraz ogólną analityczną formułę przekształcenia (4). Wynikają z niej „eleganckie” wzory na wymienione składowe pola zniekształceń. W tym celu trzeba wprowadzić pojęcie pochodnej funkcji zespolonej. Załóżmy więc „chwilowo”, że mamy do czynienia z wielomianem rzeczywistym, a dopiero w wyniku wyznaczenia pochodnej „ujawnimy tę zatajoną prawdę”. Pochodna będzie zatem wielomianem zespolonym stopnia n – 1, zaś jej wartości będą parami liczb określonymi dla konkretnych argumentów (x, y). Oznaczając formalnie: dZ/dz = (fx, fy), wyrażamy szukane składowe pola zniekształceń wzorami:
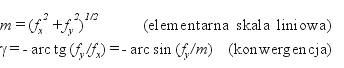 (6) Formuły (4) i (6) aplikuje się też do odwzorowania: elipsoida–płaszczyzna, ale wtedy punkty powierzchni elipsoidy muszą być określone w układzie tzw. współrzędnych izometrycznych (zob. np. [5]).
Opracowanie 2006
|  nadchodzące wydarzenia
nadchodzące wydarzenia
 zobacz pozostałe
zobacz pozostałe