|
Janusz Śledziński
Elementy orbity satelity
Wyznaczanie położenia punktów na podstawie obserwacji GPS należy do zadań dynamicznych, tj. takich, dla których rozwiązania trzeba znać współrzędne przestrzenne satelitów w momencie obserwacji. Współrzędne te określa się na podstawie elementów orbity nadawanych przez wszystkie satelity GPS w tzw. almanachu. Co to są elementy orbity? Ile ich jest i co one definiują?
Przybliżenie ruchu satelity ruchem keplerowskim. Wychodząc z prawa powszechnego ciążenia sformułowanego przez Isaaka Newtona (1643-1727), w mechanice teoretycznej wyprowadza się równanie ruchu keplerowskiego punktu materialnego poruszającego się w centralnym polu grawitacyjnym. Keplerowskim nazywamy taki ruch satelity wokół ciała centralnego (Ziemi), który odbywa się wyłącznie pod wpływem centralnych sił grawitacyjnych ściśle zgodnie z prawami Keplera (1571-1630). Opisuje on tylko w pewnym przybliżeniu rzeczywisty ruch sztucznego satelity, nie mamy bowiem tak idealnej sytuacji, o jakiej jest mowa w powyższej definicji. Rzeczywisty ruch satelity odbywa się w niecentralnym polu grawitacyjnym spowodowanym skomplikowanym kształtem Ziemi odbiegającym znacznie od kuli oraz nierównomiernym rozkładem mas w jej wnętrzu. Efekt niecentralności pola grawitacyjnego potęgowany jest także przez grawitacyjny wpływ innych stosunkowo bliskich ciał niebieskich, np. Księżyca i planet. Ponadto na ruch sztucznego satelity mają wpływ nie tylko siły grawitacyjne, lecz również m.in. opór atmosfery, siły magnetyczne, ciśnienie światła słonecznego. Podstawową konsekwencją analizy ruchu keplerowskiego sztucznego satelity jest to, że wszystkie wielkości określające ten ruch (m.in. kształt i wielkość orbity satelity oraz jej położenie w przestrzeni) są stałe w czasie.
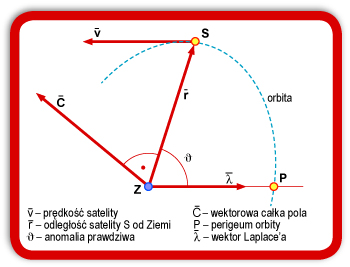
Rys. 1. Rozwiązania równania ruchu
Równanie ruchu keplerowskiego. Jest ono wektorowym równaniem różniczkowym drugiego rzędu i ma postać:
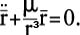
Jego rozwiązaniami powinny być dwa stałe i niezależne wektory lub sześć niezależnych wielkości skalarnych, które będą wynikiem dwukrotnego całkowania tego równania. Wielkości te powinny określać tor poruszającego się ciała (orbitę), a także wiązać jego ruch z czasem i pozwolić na wyznaczenie położenia i prędkości satelity w każdym momencie. Owe sześć wielkości nazywać będziemy elementami orbity satelity.
W wyniku całkowania równania ruchu otrzymujemy dwa stałe wektory: tzw. wektorową całkę pola C oraz tzw. wektor Laplace’a λ. Dodatkowo uzyskać możemy jeszcze jedną całkę – skalarną stałą energii h. Zatem na podstawie całkowania równania ruchu otrzymujemy 7 wielkości skalarnych: trzy składowe wektora C, trzy składowe wektora Laplace’a λ oraz stałą energii. Z teorii równań różniczkowych wiemy jednak, że rozwiązaniami równania mogą być tylko stałe całki niezależne. Natomiast uzyskane wielkości związane są dwiema zależnościami. Wynika to stąd, że z siedmiu znalezionych wielkości można wziąć dowolnie tylko 5, a dwie pozostałe muszą spełniać owe zależności.
Wektor C = r × v jest iloczynem wektorowym dwóch wektorów – odległości do satelity r oraz prędkości satelity v. Oba te wektory leżą w płaszczyźnie orbity (rys. 1), zatem stały wektor C jako iloczyn wektorowy musi być prostopadły do płaszczyzny orbity, a to oznacza, że płaszczyzna orbity zajmuje stałe położenie w przestrzeni. Wektor Laplace’a leży w płaszczyźnie orbity i jest skierowany do punktu perigeum orbity (określa położenie punktu perigeum). Zatem wektory C i λ są zawsze do siebie prostopadłe (co stanowi jedną ze wspomnianych zależności między całkami równania ruchu).
Sześć elementów orbity. Elementy orbity są wielkościami pozwalającymi określić w każdym momencie położenie satelity w przestrzeni i jego prędkość (rys. 2).
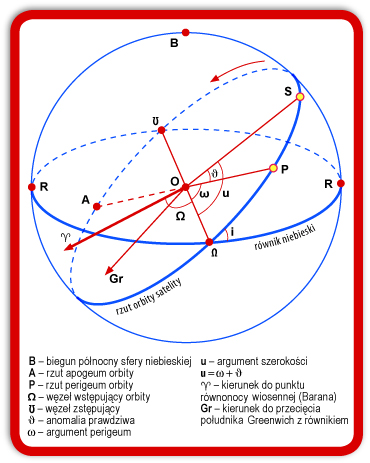
Rys. 2. Elementy orbity
Położenie płaszczyzny orbity w przestrzeni określają dwa elementy orbity:
i – nachylenie płaszczyzny orbity względem równika,
? – położenie węzła wstępującego orbity (tj. punktu, w którym rzut orbity na sferę niebieską przecina się z równikiem niebieskim; w punkcie tym satelita przechodzi z półkuli południowej na północną); elementem orbity może być albo długość geograficzna węzła wstępującego λ? (liczona od południka Greenwich), albo rektascensja węzła wstępującego α? (liczona od punktu równonocy wiosennej, czyli punktu Barana).
Położenie orbity w jej płaszczyźnie określa jeden element orbity pokazujący położenie punktu perigeum, czyli punktu orbity położonego najbliżej Ziemi; elementem tym jest odległość kątowa punktu perigeum od węzła wstępującego liczona wzdłuż orbity:
ω – argument perigeum orbity.
Wielkość i kształt orbity określają (w najbardziej ogólnym przypadku orbity eliptycznej) dwa elementy; zazwyczaj są to:
a – duża półoś orbity,
e – mimośród orbity.
Powiązanie ruchu satelity z czasem następuje przez określenie czasu przejścia satelity przez wybrany punkt orbity (w zależności od rodzaju orbity i jej nachylenia względem równika mogą to być: perigeum orbity, węzeł wstępujący orbity, przecięcie z południkiem Greenwich itd.).
Należy wspomnieć, że niektóre rodzaje orbit nie wymagają określania sześciu elementów. Na przykład do zdefiniowania orbity kołowej potrzebne są tylko 4 z nich. Nie posiada ona bowiem punktu perigeum – nie występuje więc argument perigeum ω. Z kolei jej mimośród wynosi 0, więc wielkość orbity kołowej określa tylko jeden element – promień r.
Prof. Janusz Śledziński był pracownikiem naukowym Instytutu Geodezji Wyższej i Astronomii Geodezyjnej Politechniki Warszawskiej, 2010
|  nadchodzące wydarzenia
nadchodzące wydarzenia
 zobacz pozostałe
zobacz pozostałe