Matematyczna konstrukcja map

Robert Olszewski, Paweł Kowalski, Andrzej Głażewski

Konstrukcja matematyczna mapy opiera się na przyjętej w odwzorowaniu powierzchni odniesienia, której zadaniem jest najlepsza aproksymacja fizycznej powierzchni Ziemi. Powierzchnią najlepiej oddającą/odzwierciedlającą kształt Ziemi jest geoida (powierzchnia ekwipotencjalna). Powierzchnia ta nie posiada jednak prostego opisu matematycznego, dlatego nie buduje się na niej układów współrzędnych. W geodezji i kartografii jako powierzchnie odniesienia przyjęto zatem elipsoidę, sferę lub płaszczyznę. Najprostszą bryłą matematyczną, której kształt jest najbardziej zbliżony do kształtu geoidy, jest elipsoida obrotowa o niewielkim spłaszczeniu (różnica długości półosi nie przekracza 22 km).
Elipsoida obrotowa jest określona przez dwa parametry, w tym przynajmniej przez jeden długościowy (np. a i b lub przez półoś a i spłaszczenie f). Parametry te mają wartości liczbowe, które otrzymuje się na podstawie odpowiednich pomiarów geodezyjnych, prowadzonych obecnie z wykorzystaniem satelitarnych systemów wyznaczania pozycji (GNSS), jak np. GPS. Ustalenie rozmiarów elipsoidy, której kształt byłby najbardziej zbliżony do rzeczywistego kształtu Ziemi, posiada wielkie znaczenie zarówno teoretyczne, jak i praktyczne, np. przy opracowaniach dokładnych map topograficznych, wymagających redukowania pomiarów wykonywanych na powierzchni Ziemi na powierzchnię elipsoidy.

Ponieważ mała oś elipsoidy jest krótsza od średnicy równika ziemskiego w przybliżeniu o 43 km, to dla wielu prac niewymagających specjalnej dokładności za powierzchnię odniesienia przyjmuje się sferę kuli, której promień wynosi około 6371 km, powierzchnia zaś około 510 mln km². Dotyczy to zwłaszcza zastosowań kartograficznych w odniesieniu do map małoskalowych (np. w atlasach), obejmujących zwykle duże obszary (państwa, kontynenty, świat).
Dla stosunkowo małych obszarów można zaniedbać w ogóle krzywiznę Ziemi i za powierzchnię odniesienia przyjąć płaszczyznę. Tak małe obszary mogą być interpretowane jako płaskie i odwzorowywane bez zniekształceń (powierzchnią odniesienia jest płaszczyzna). W ogólnym przypadku należy dokonać odwzorowania kartograficznego, które za pomocą formuł matematycznych gwarantuje wzajemnie jednoznaczną odpowiedniość punktową pomiędzy elementami zlokalizowanymi na powierzchni oryginału (powierzchni odniesienia) i ich odpowiednikami na powierzchni obrazu (płaszczyźnie odwzorowawczej). Odwzorowanie takie wyraża związki pomiędzy układami współrzędnych związanymi z obiema powierzchniami: oryginału i obrazu. Układem wyjściowym w opracowaniach kartograficznych jest zwykle układ współrzędnych geodezyjnych (B, L), budowany na elipsoidzie lub układ współrzędnych geograficznych (φ, λ), związany ze sferą. Układem związanym z płaszczyzną obrazu jest układ współrzędnych prostokątnych płaskich (X, Y), definiowany w nawiązaniu do elementów siatki kartograficznej.

Stosuje się wiele różnych typów odwzorowań kartograficznych, które klasyfikuje się m.in. ze względu na typy wielkości podlegających zniekształceniom odwzorowawczym. Wiadomo, że odwzorowanie, które zachowywałoby wszystkie rodzaje wielkości (długości linii, kąty i powierzchnie) nie istnieje, co wynika z nierozwijalności najczęściej stosowanych powierzchni oryginału (elipsoidy bądź sfery) na płaszczyznę. Wybór odwzorowania zależy zawsze od wymogów, jakim powinna odpowiadać mapa. Na mapach topograficznych odwzorowanie kartograficzne powinno zapewnić wiernokątność, tj. zgodność mierzonych kątów w tym samym punkcie na obu powierzchniach, co wynika z wojskowego rodowodu tych map, a także odpowiednią (dla danego obszaru) optymalizację rozkładu zniekształceń długości. Porównanie wielkości na powierzchni odniesienia (oryginał) i płaszczyźnie obrazu daje współczynnik skali zwany lokalno-kierunkową skalą w odwzorowaniu (może to być np. lokalno-kierunkowa skala długości). Współczynnik ten oscyluje wokół wartości równej 1, którą przyjmuje jedynie w miejscach (i w kierunkach) odwzorowanych izometrycznie (zniekształcenia długości nie występują).

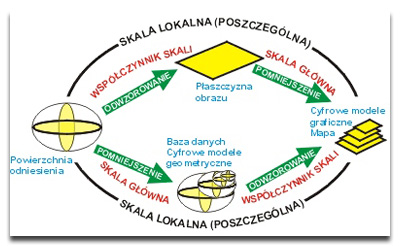
Współczynniki skalowe na poszczególnych etapach opracowania mapy

Ostatni etap matematycznego konstruowania mapy polega na pomniejszeniu płaszczyzny obrazu do rozmiarów przyjętych w założeniach według współczynnika skali głównej mapy. To właśnie ten współczynnik, mówiący o stopniu zmniejszenia płaszczyzny obrazu, niezależny od miejsca i kierunku pomiaru, stały w każdym punkcie mapy, jest uwidoczniony na mapach w postaci opisu bądź podziałki. Skala główna mapy jest zawsze wyznacznikiem jej szczegółowości, dotyczy to zwłaszcza baz danych i map elektronicznych, których skala prezentacji jest wielkością chwilową. Jak widać na rysunku, można też porównać wielkości (np. długości linii) na mapie i na powierzchni oryginału (powierzchni odniesienia), co da współczynnik skali lokalnej (poszczególnej). Skala lokalna na mapie jest więc iloczynem stopnia pomniejszenia płaszczyzny obrazu (skali głównej mapy) i skali lokalno-kierunkowej w odwzorowaniu. Jej wartości są zależne od rozkładu zniekształceń odwzorowawczych (skala lokalno-kierunkowa w odwzorowaniu jest zmienna), a w miejscach odwzorowanych izometrycznie jest ona równa skali głównej mapy.

Dr Robert Olszewski, dr Paweł Kowalski i dr Andrzej Głażewski są pracownikami Zakładu Kartografii Politechniki Warszawskiej

Opracowanie zamieszczono na Geoforum w marcu 2006 r.