|
Jerzy Balcerzak, Paweł Pędzich
Kartografia matematyczna jest działem kartografii zajmującym się opracowaniem podstaw matematycznych odwzorowań powierzchni Ziemi na mapach oraz podstawami matematycznymi wykonywania pomiarów na mapach. Jej tradycje sięgają kilku tysięcy lat. Jednym z pierwszych znanych dzieł, w którym podejmowano tematykę odwzorowań kartograficznych, była Geografia Klaudiusza Ptolomeusza, astronoma i geografa, żyjącego w II wieku w Aleksandrii. W pierwszym tomie dzieła Ptolemeusz wyłożył ówczesne podstawy kartografii matematycznej.
Różne kryteria odwzorowań kartograficznych
Problemem wiernego odwzorowania powierzchni Ziemi na płaszczyźnie zajmowali się najwybitniejsi matematycy, m.in. Euler, Lagrange, Gauss, Czebyszew. Przez wiele lat największym wyzwaniem podejmowanym przez kartografów-matematyków było poszukiwanie odwzorowań charakteryzujących się w miarę możliwości najmniejszymi zniekształceniami.
Jednak minimalne zniekształcenia nie są jedynym kryterium przy doborze odwzorowań kartograficznych. Często ważniejszym kryterium jest przeznaczenie i wygoda użytkowania mapy. Na przykład do tworzenia map nawigacyjnych od XVI wieku po dzień dzisiejszy stosuje się odwzorowanie Mercatora. W odwzorowaniu tym linia przecinająca południki na powierzchni kuli pod stałym kątem (loksodroma) odwzorowuje się na linię prostą. Ułatwia to znakomicie prowadzenie nawigacji. Z kolei w geodezji i topografii oczekuje się zachowania kątów, stąd zastosowanie mają odwzorowania konforemne – Gaussa-Krügera, UTM.
Pojęcie powierzchni odniesienia w kartografii
W kartografii matematycznej za powierzchnię odniesienia przyjmuje się elipsoidę lub sferę. Są to tak zwane powierzchnie oryginału w odwzorowaniach kartograficznych, które w procesie matematycznego przyporządkowania odwzorowuje się na płaszczyznę w celu opracowania mapy. Sfera jako powierzchnia oryginału stosowana jest do opracowania map małoskalowych (np. zamieszczanych w atlasach geograficznych), natomiast elipsoida – do map wielko- i średnioskalowych (np. mapa zasadnicza, mapy topograficzne).
Elipsoida odniesienia wyznaczana jest na podstawie pomiarów geodezyjnych, grawimetrycznych i satelitarnych. Pozwalają one określić parametry opisujące kształt i wielkość elipsoidy oraz ustalić jej orientację względem bryły Ziemi. Wraz z rozwojem technologii pomiarowych pojawiały się elipsoidy lokalne (m.in. Bessela, Hayforda, Krasowskiego), a następnie globalne (GRS’80, WGS’84).
Obecnie do opracowania map stosuje się dwie elipsoidy wchodzące w skład dwóch niewiele różniących się układów odniesienia: WGS’84 oraz GRS’80. Parametry metryczne określające kształt i wielkość tych elipsoid praktycznie nie różnią się między sobą.
Na powierzchniach odniesienia wprowadza się układy współrzędnych, które pozwalają jednoznacznie określić położenie punktu. Najstarszym ze znanych układów współrzędnych jest układ współrzędnych geograficznych j, l stosowany na sferze. Położenie punktu na jej powierzchni określa się za pomocą pary współrzędnych: szerokości geograficznej j i długości geograficznej l. Na elipsoidzie natomiast stosuje się układ współrzędnych geodezyjnych B, L, w którym położenie punktu określa się za pomocą szerokości geodezyjnej B i długości geodezyjnej L.
Do określania współrzędnych punktu na elipsoidzie oraz kuli stosuje się także ortokartezjańskie układy współrzędnych prostokątnych. Początek takiego układu znajduje się w środku elipsoidy lub kuli, oś z pokrywa się z osią obrotu elipsoidy, oś x leży w płaszczyźnie wybranego południka początkowego, a oś y jest ortogonalna do osi x i z, tworząc prawoskrętny układ oxyz.
Odwzorowanie kartograficzne
Odwzorowaniem kartograficznym jest wzajemnie jednoznaczne przyporządkowanie punktów powierzchni oryginału (elipsoidy lub sfery) punktom płaszczyzny obrazu, w której tworzona jest mapa. Odwzorowanie definiuje się za pomocą funkcji matematycznych wyrażających wzajemną zależność pomiędzy współrzędnymi powierzchni oryginału a współrzędnymi prostokątnymi płaskimi mapy. Odwzorowanie sfery w płaszczyznę możemy zapisać ogólnie w następującej postaci:
x = x(j, l)
y = y(j, l),
natomiast elipsoidy w płaszczyznę:
x = x(B,L)
y = y(B,L).
Skale i zniekształcenia odwzorowawcze
Mapę opracowuje się w danej skali m 0 = 1:M, zwanej skalą główną odwzorowania. Jest to współczynnik pomniejszenia współrzędnych x, y określonych za pomocą podanych wyżej funkcji. Realizowane jest w ten sposób pomniejszenie obrazu powierzchni odwzorowywanej. Często w literaturze spotyka się definicję skali głównej sformułowaną jako stosunek „myślowego” pomniejszenia wymiarów powierzchni oryginału (elipsoidy lub kuli) przed rozpoczęciem procesu odwzorowania. Skala ta wyraża stosunek zmniejszenia wymiarów liniowych powierzchni oryginału. Skala główna m0 jest zachowana w odwzorowaniu na mapie tylko w tych punktach, w których nie występują zniekształcenia odwzorowawcze.
Ponieważ nie jest możliwe rozwinięcie powierzchni kuli lub elipsoidy w płaszczyznę bez zniekształceń, to jednym z zadań kartografii matematycznej jest badanie wartości zniekształceń odwzorowawczych długości, kątów i pól. Do określenia wielkości zniekształceń stosuje się różne miary. Miary te pozwalają na wyznaczanie wartości zniekształceń lokalnych w otoczeniu danego punktu, jak również zniekształceń globalnych w pewnym obszarze. Podstawową miarą stosowaną w kartografii do badania lokalnych zniekształceń odwzorowawczych jest elementarna skala zniekształceń wyrażająca stosunek odpowiadających sobie elementarnych wielkości na powierzchni oryginału i płaszczyźnie obrazu. Wykorzystywana jest ona głównie do wyznaczania zniekształceń długości (elementarna skala zniekształceń długości m = ds'/ds) i pól (elementarna skala zniekształceń pól p = dP'/dP), rzadziej do wyznaczania zniekształceń kątów. Zniekształcenie kąta określa się częściej jako różnicę pomiędzy kątem na oryginale a jego obrazem. Elementarna skala zniekształceń długości m = ds'/ds jest funkcją trzech zmiennych: dwóch współrzędnych określających położenie punktu na oryginale (B, L na elipsoidzie lub j, l na kuli) oraz kierunku w tym punkcie. Stąd też nazywana jest również skalą lokalno-kierunkową. W szczególnym przypadku – odwzorowania wiernokątnego – skala zniekształceń długości nie zależy od kierunku w danym punkcie, mówimy wówczas o skali lokalnej.
W kartografii wprowadza się też pojęcie skali poszczególnej odwzorowania, która wyraża się wzorem: mp = m m0 .
Skala poszczególna mp wyraża więc iloczyn skali głównej i elementarnej skali zniekształceń długości odwzorowania m. Wzajemne zależności pomiędzy skalami ilustruje rys. 1.

Rys. 1. Skala główna, elementarna i poszczególna w odwzorowaniu kartograficznym
Miarą, która w sposób kompleksowy wyraża zniekształcenia odwzorowawcze w otoczeniu danego punktu, jest elipsa zniekształceń odwzorowawczych, tzw. wskaźnica Tissota. Oddaje ona wartości elementarnych skal zniekształceń długości we wszystkich kierunkach w danym punkcie. Powstaje w wyniku odwzorowania okręgu jednostkowego wyznaczonego w płaszczyźnie stycznej danego punktu powierzchni oryginału (sfery lub elispsoidy) w płaszczyznę obrazu. Elipsa zniekształceń odwzorowawczych zawiera w sobie informacje o wartościach zniekształceń odwzorowawczych długości, kątów i pól. Promień wodzący elipsy jest elementarną skalą zniekształceń długości w danym kierunku, jej półosie wyrażają ekstremalne (minimum i maksimum) wartości skal zniekształceń długości. Wielkość spłaszczenia elipsy informuje o zniekształceniach kątowych. Im bardziej elipsa jest spłaszczona, tym większe maksymalne zniekształcenia kątów występują w danym punkcie. Natomiast pole powierzchni elipsy wyraża lokalne zniekształcenia pól powierzchni w odwzorowaniu. Rysunek elipsy zniekształceń odwzorowawczych stosuje się do graficznej prezentacji zniekształceń. Wykreślone w węzłach siatki kartograficznej lub dowolnie wybranych punktach informują o zniekształceniach lokalnych (w otoczeniu tych punktów). Zbiór elips rozmieszczonych w miarę równomiernie na określonym obszarze pozwala przedstawić charakterystykę rozkładu zniekształceń odwzorowawczych w całym odwzorowanym obszarze. Przykład graficznej prezentacji rozkładu zniekształceń odwzorowawczych (w odwzorowaniu Sansona) z zastosowaniem elips przedstawia rys. 2.

Rys. 2 Elipsy zniekształceń odwzorowawczych w odwzorowaniu Sansona
Zniekształcenia odwzorowawcze mogą być prezentowane również za pomocą izolinii zniekształceń. Są to linie stałej wartości określonego typu zniekształcenia, np. ekstremalnych zniekształceń długości, ekstremalnych zniekształceń kątów lub pól. Przykład graficznej prezentacji zniekształceń odwzorowawczych w odwzorowaniu Soldnera całej Polski z zastosowaniem metody izolinii (izolinie maksymalnych zniekształceń długości) przedstawia rys. 3.

Rys. 3. Izolinie maksymalnych zniekształceń długości w odwzorowaniu Soldnera
Klasyfikacje odwzorowań kartograficznych
Klasyfikując odwzorowania kartograficzne, najczęściej uwzględnia się kształt siatek kartograficznych oraz charakter zniekształceń odwzorowawczych. Za względu na kryterium kształtu siatek kartograficznych wyróżnia się następujące typy odwzorowań kartograficznych:
-
azymutalne, w których równoleżniki odwzorowują się na koncentryczne okręgi, a południki w postaci pęku prostych, rys. 4a, 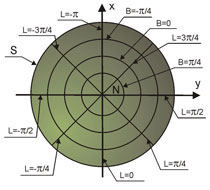 Rys. 4a. Odwzorowanie azymutalne Rys. 4a. Odwzorowanie azymutalne
- walcowe – równoleżniki odwzorowują się na odcinki linii prostych równoległych do osi y, południki na proste równoległe do osi x układu współrzędnych płaskich, rys. 4b,

Rys. 4b. Odwzorowanie walcowe
- stożkowe – równoleżniki odwzorowują się na łuki okręgów koncentrycznych, południki w postaci pęku prostych, rys. 4c,

Rys. 4c. Odwzorowanie stożkowe
- pseudoazymutalne – równoleżniki odwzorowują się na koncentryczne okręgi, południki w postaci krzywych, rys. 4d,
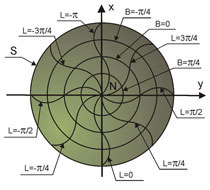
Rys. 4d. Odwzorowanie pseudoazymutalne
- pseudowalcowe – równoleżniki odwzorowują się na odcinki linii prostych równoległych do osi y, południki na łuki krzywych, rys. 4e,

Rys. 4e. Odwzorowanie pseudowalcowe
- pseudostożkowe – równoleżniki odwzorowują się na łuki okręgów koncentrycznych, południki na łuki krzywych, rys. 4f,

Rys. 4f. Odwzorowanie pseudostożkowe
- wielostożkowe – równoleżniki odwzorowują się na łuki okręgów ekscentrycznych, południki na łuki krzywych, rys. 4g.
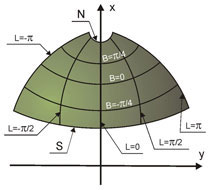
Rys. 4g. Odwzorowanie wielostożkowe
Ze względu na kryterium zniekształceń odwzorowawczych wyróżnia się odwzorowania:
- izometryczne – nie występują żadne zniekształcenia,
- wiernokątne – kąty odwzorowują się bez zniekształceń,
- wiernopolowe – pola powierzchni są zachowane bez zniekształceń,
- wiernoodległościowe – długości w określonym kierunku zostają zachowane.
Mimo że izometryczne odwzorowania kartograficzne kuli lub elipsoidy w płaszczyznę nie istnieją, jest to bardzo ważny typ odwzorowań, ponieważ w płaszczyźnie obrazu mogą występować punkty lub linie odwzorowujące się izometrycznie, są to linie zerowych zniekształceń. Ma to istotne znaczenie w projektowaniu odwzorowań kartograficznych o możliwie najmniejszych zniekształceniach w zadanym obszarze.
Na osobną uwagę zasługują odwzorowania konforemne. Są to odwzorowania równokątne, których metoda konstrukcji oparta jest na teorii funkcji zmiennej zespolonej. W tworzeniu odwzorowań kartograficznych konforemnych ma zastosowanie twierdzenie o następującej treści: jeżeli na powierzchni oryginału – elipsoidzie lub sferze – wprowadzimy współrzędne izometryczne q i L oraz w płaszczyźnie obrazu współrzędne izometryczne x i y, to dowolne odwzorowanie konforemne jest określone związkiem
x + iy = f(z) = f(q + iL),
gdzie:
f(q + iL)
jest pewną funkcją analityczną zmiennej zespolonej o pochodnej różnej od zera. Siatka współrzędnych izometrycznych posiada taką własność, że jednakowe przyrosty współrzędnych powodują proporcjonalnie jednakowe przesunięcia liniowe punktów wzdłuż południków i równoleżników elipsoidy lub kuli i odwrotnie: jednakowe przesunięcia liniowe punktów wzdłuż południków i równoleżników powodują jednakowe zmiany współrzędnych zgodnie ze wzorem:
ds2 = σ2 (dq2 + dL2).
Ponieważ współrzędne geograficzne j, l na sferze oraz współrzędne geodezyjne B, L na elipsoidzie nie są współrzędnymi izometrycznymi, to w procesie tworzenia odwzorowań konforemnych tych powierzchni wprowadza się na nich tzw. szerokość izometryczną q.
Oprócz wymienionych wyżej typów odwzorowań należy wspomnieć o pewnych aspektach odwzorowań kartograficznych wynikających z różnych położeń powierzchni rozwijalnych na płaszczyźnie (walec, stożek) względem powierzchni kuli. W związku z tym wyróżnia się odwzorowania normalne, ukośne i porzeczne. Wymienione trzy aspekty odwzorowań kartograficznych ilustruje rys. 5.
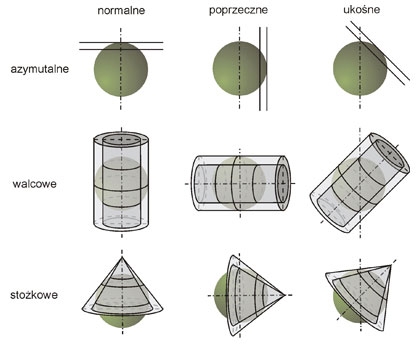
Rys. 5. Odwzorowania normalne, ukośne i poprzeczne
Metody tworzenia odwzorowań kartograficznych
Metody tworzenia odwzorowań kartograficznych możemy podzielić na trzy główne grupy:
Konstrukcyjne – odwzorowanie jest realizowane z wykorzystaniem zasad rzutowania powierzchni oryginału na płaszczyznę, pobocznicę walca lub stożka. Wśród nich wyróżnia się trzy podstawowe rzuty: ortograficzny, stereograficzny i środkowy.
Analityczne – polegają na analitycznym rozwiązywaniu stosownych układów równań różniczkowych. Podajemy wówczas ogólne warunki, które ma spełniać odwzorowanie, np. odwzorowanie ma być równokątne i walcowe. Na tej podstawie układamy odpowiednie równanie różniczkowe. Po jego rozwiązaniu w następnym kroku wyznaczamy pewne stałe na podstawie warunków szczegółowych, np. żądania, aby dany równoleżnik odwzorował się izometrycznie.
Numeryczne – często odwzorowania kartograficzne otrzymujemy w wyniku rozwinięcia funkcji odwzorowawczych na szeregi potęgowe lub trygonometryczne, lub stosując odpowiednie wielomiany aproksymacyjne.
Minimalizacja zniekształceń w odwzorowaniach kartograficznych
Przez wiele lat największym wyzwaniem podejmowanym przez kartografów-matematyków było poszukiwanie odwzorowań o jak najmniejszych zniekształceniach. Posługiwano się różnymi kryteriami pozwalającymi na minimalizację zniekształceń odwzorowawczych. Można wspomnieć tutaj takie kryteria, jak: Jordana, Tissota, Airy i Czebyszewa. Wśród nich na uwagę zasługuje szczególnie ostatnie z wymienionych. Czebyszew sformułował twierdzenie, że najmniejsze zniekształcenia odwzorowawcze uzyskamy w odwzorowaniu danego obszaru, przyjmując na jego brzegu stałą skalę zniekształceń długości. Twierdzenie to zostało udowodnione w odniesieniu do odwzorowań konforemnych w kilkadziesiąt lat po śmierci Czebyszewa. Natomiast zagadnienie minimalizacji zniekształceń w odwzorowaniach innego typu, np. wiernopolowych, pozostaje nadal otwarte.
Siatkę kartograficzną oraz izolinie zniekształceń długości w odwzorowaniu Czebyszewa obszaru Polski przedstawia rys. 6.
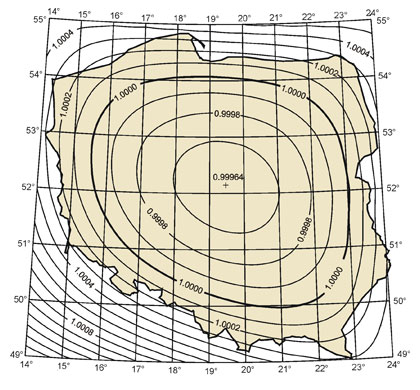
Rys. 6. Odwzorowanie Czebyszewa obszaru Polski
Z rysunku widać, że maksymalna różnica zniekształceń liniowych w odwzorowaniu wiernokątnym obszaru Polski wynosi około 72 cm/km. Z twierdzenia Czebyszewa oraz przedstawionych wyników obliczeń wynika, że uzyskanie znacznego zmniejszenia zniekształceń odwzorowawczych w jednolitym odwzorowaniu Polski będzie mało prawdopodobne.
Odwzorowanie Gaussa-Krügera oraz Uniwersalne Poprzeczne Mercatora (UTM – Universal Transverse Mercator)
Wiernokątne odwzorowanie elipsoidy, które w późniejszych czasach zyskało nazwę Gaussa-Krügera, zostało opracowane przez matematyka niemieckiego Carla Friedricha Gaussa i użyte przez niego w latach 1820-30 do obliczenia wyników triangulacji Hanoweru. Na podstawie notatek i rękopisów Gaussa geodeta niemiecki Louis Krüger gruntownie dopracował metodę tego odwzorowania i opublikował w roku 1912. Stąd wzięła się nazwa odwzorowanie Gaussa-Krügera.
Jest to odwzorowanie konforemne powierzchni elipsoidy obrotowej spłaszczonej w płaszczyznę spełniające dwa warunki:
1. południk osiowy odwzorowuje się na odcinek linii prostej osi rzędnych x,
2. elementarna skala zniekształceń długości na południku osiowym jest stała i równa jedności, tzn., że południk osiowy odwzorowuje się bez zniekształceń (izometrycznie).
Często w literaturze podawana jest interpretacja geometryczna tego odwzorowania, zgodnie z którą jest to wiernokątne, walcowe, styczne, poprzeczne odwzorowanie elipsoidy obrotowej spłaszczonej w płaszczyznę.
Zaproponowane w latach II wojny światowej w Ameryce odwzorowanie UTM stanowi pewną modyfikację odwzorowania Gaussa-Krügera. UTM jest także odwzorowaniem konforemnym elipsoidy w płaszczyznę z południkiem osiowym odwzorowującym się na odcinek linii prostej ze stałą skalą zniekształceń długości, lecz wartość tej skali jest mniejsza od jedności i równa m0=0,9996. Zależność pomiędzy współrzędnymi w odwzorowaniu Gaussa-Krügera a współrzędnymi w odwzorowaniu UTM zgodnie z powyższym przedstawiają wzory:
xUTM = m0 × xGK
yUTM = m0 × yGK.
Odwzorowanie UTM stosowane jest do 6-stopniowych stref południkowych pomiędzy równoleżnikami -80° do +80°.
Odwzorowania Gaussa-Krügera i UTM – ze względu na duże zniekształcenia długości – stosowane są w kilkustopniowych pasach południkowych. Odwzorowania te są obecnie powszechnie stosowane w geodezji i topografii. W Polsce do tworzenia map topograficznych w układzie 1992 i UTM oraz mapy zasadniczej w układzie 2000.
Odwzorowanie quasi-stereograficzne
Metodę tworzenia odwzorowania stereograficznego dla elipsoidy podał w 1924 roku astronom francuski Roussilhe. Adaptując to odwzorowanie do obszaru Polski, profesor dr Lucjan Grabowski z Politechniki Lwowskiej zaproponował stosowne wzory matematyczne. W 1930 roku F. Biernacki i J. Słomczyński (oficerowie ówczesnego Wojskowego Instytutu Geograficznego) zastosowali to odwzorowanie w pracach geodezyjnych i kartograficznych obszaru Polski. Po II wojnie światowej znalazło zastosowanie przede wszystkim do tworzenia map topograficznych i zasadniczych w układzie 1965 (strefy odwzorowawcze 1-4) oraz map topograficznych w układzie GUGiK 80.Odwzorowanie quasi-stereograficzne jest odwzorowaniem konforemnym, azymutalnym powierzchni elipsoidy obrotowej spłaszczonej w płaszczyznę. W ograniczonym obszarze odpowiada ono stereograficznemu odwzorowaniu kuli o promieniu

wyznaczonym w punkcie głównym odwzorowania, tj. punkcie styczności płaszczyzny odwzorowania do elipsoidy.
Prace teoretyczne nad własnościami odwzorowania Roussilhe’a wykazały, że może być ono powiązane z odwzorowaniem Gaussa-Krügera. Otrzymano prostą pojęciowo i sprawną numerycznie metodę bez konieczności rozwijania na szeregi. Metoda ta pozwala ponadto na odwzorowanie dowolnie dużego obszaru z całą elipsoidą włącznie.
Odwzorowanie Mercatora
Twórcą tego odwzorowania był kartograf i matematyk Gerhard Kremer, znany powszechnie jako Mercator. W 1569 roku sporządził mapę świata w odwzorowaniu równokątnym walcowym normalnym kuli w płaszczyznę. Odwzorowanie stosuje się w ograniczonym pasie równoleżnikowym, ponieważ bieguny N i S odwzorowują się w nieskończoności. Ważną własnością odwzorowania Mercatora jest fakt, że loksodroma (linia przecinająca południki pod stałym kątem) odwzorowuje się na prostą przecinającą obrazy południków pod stałym kątem. Ze względu prostotę i łatwość użytkowania odwzorowania Mercatora powszechnie stosowane jest do tworzenia map nawigacyjnych.
Układy współrzędnych prostokątnych płaskich stosowane w Polsce
Odwzorowania kartograficzne stanowią podstawę tworzenia różnych układów współrzędnych prostokątnych płaskich stosowanych w pracach geodezyjnych i kartograficznych. Układy te są wprowadzane w celu ujednolicenia urzędowych opracowań kartograficznych i geodezyjnych pod względem podstaw matematycznych. W Polsce na przestrzeni ostatnich pięćdziesięciu lat stosowano 6 państwowych układów współrzędnych: 1942, 1965, GUGiK80, 1992, 2000, UTM.
- Układ 1942 został wprowadzony w 1953 r. Był przeznaczony do opracowań wojskowych. Wykonywano w nim prace geodezyjne i kartograficzne oraz wydawano wojskowe mapy topograficzne. Jego użytkowanie zakończono ok. roku 1990, ale do roku 1997 wydawano jeszcze mapy topograficzne. W układzie 1942 zastosowano odwzorowanie Gaussa-Krügera elipsoidy Krasowskiego. Układ stosowany był w dwóch wersjach: strefy 6-stopniowe (do opracowania map topograficznych), strefy 3-stopniowe (do map wielkoskalowych).
- Układ 1965 wprowadzony w 1968 r. był przeznaczony do opracowań topograficznych i geodezyjnych. W układzie tym występuje podział na pięć stref odwzorowawczych, których zasięg oparty był na ówczesnym podziale administracyjnym kraju. W strefach o numerach 1-4 zastosowano odwzorowanie quasi-stereograficzne, natomiast w strefie piątej – odwzorowanie Gaussa-Krügera. Jako powierzchnię odniesienia przyjęto elipsoidę Krasowskiego.
- Układ GUGiK 80 wprowadzony był w Polsce na początku lat 80. do opracowania map topograficznych w skalach mniejszych od 1:50 000. Układ ten nie był ujawniony na mapach. Mapy topograficzne posiadały siatkę kartograficzną, natomiast nie umieszczono na nich siatki kilometrowej. W układzie tym wykonano mapę topograficzną w skali 1:100 000 oraz mapę przeglądową w skali 1:500 000. Zastosowano odwzorowanie quasi-stereograficzne jednostrefowe dla całej Polski. Jako powierzchnię odniesienia przyjęto elipsoidę Krasowskiego (niektóre źródła podają elipsoidę Bessela).
- Układ 1992 stosowano w Polsce od 1995 r. do opracowania cywilnych map topograficznych, choć oficjalnie został zatwierdzony ustawą dopiero w roku 2000. W układzie tym zastosowano odwzorowanie Gaussa-Krügera w jednej 10-stopniowej strefie odwzorowawczej. Przyjęto skalę zniekształceń długości na południku osiowym równą 0,9993, co daje w niektórych miejscach zniekształcenia długości równe -70 cm/km. Na wschodnich krańcach Polski występują maksymalne zniekształcenia równe +90 cm/km. Jako powierzchnię odniesienia zastosowano elipsoidę GRS80.
- Układ 2000 zatwierdzony tą samą ustawą z roku 2000 co układ 1992 i przeznaczony do prac geodezyjnych. W układzie tym zastosowano odwzorowanie Gaussa-Krügera w pasach 3-stopniowych. Jako powierzchnię odniesienia przyjęto elipsoidę GRS 80.
- Układ UTM jest układem współrzędnych prostokątnych płaskich wykorzystywanym do opracowań wojskowych. Zastosowano w nim odwzorowanie Gaussa-Krügera w pasach 6-stopniowych. Na południku osiowym przyjęto skalę zniekształceń długości równą 0,9996. Jako powierzchnię odniesienia przyjęto elipsoidę WGS84.
dr hab. Jerzy Balcerzak był dyrektorem Instytutu Fotogrametrii i Kartografii Wydziału Geodezji i Kartografii Politechniki Warszawskiej
dr Paweł Pędzich jest pracownikiem Zakładu Kartografii Wydziału Geodezji i Kartografii PW
Opracowanie zamieszczono na Geoforum w październiku 2006 r.
|
