|
Do tej pory zajmowaliśmy się formułami transformacyjnymi współrzędnych, na bazie teoretycznych modeli dotyczących elipsoid odniesienia i ich matematycznych odwzorowań. Nasze rozważania dotyczyły więc pewnych sytuacji „idealnych”, jakie leżały u podstaw projektowania układów współrzędnych. Z drugiej strony, każdy definiowany w geodezji układ współrzędnych ma sens praktyczny tylko wtedy, gdy istnieje jego fizycznie powiązanie z obiektem pomiaru (powierzchnią Ziemi) poprzez punkty osnów geodezyjnych (których współrzędne w danym układzie wyznaczono na drodze procesu pomiarowo-obliczeniowego). Pomiędzy teorią układu a jego rzeczywistą (empiryczną) realizacją, która dokonuje się w środowisku błędów pomiarowych, będzie zachodzić zatem mniej lub bardziej istotna rozbieżność. Konieczność jednoznacznych rozstrzygnięć wymusza stosowanie dodatkowych operacji korygujących owe rozbieżności. Problem będzie mieć niebawem coraz większe znaczenie praktyczne, zwłaszcza w aspekcie przetwarzania archiwalnych zasobów kartograficznych z układu „1965” do nowego układu „2000”.
Matematyka a rzeczywistość
Dla ilustracji problemu rozważmy następującadanie: Mamy dane współrzędne x, y pewnego punktu osnowy poziomej I klasy w układzie „1992”, pozyskane z nowego wyrównania sieci na elipsoidzie GRS-80. Stosując poznane formuły matematyczne, przekształcamy je na przykład do strefy 1. układu „1965” (pamiętamy, że na drodze przekształcenia uwzględniamy przybliżoną informację o wysokości elipsoidalnej punktu):
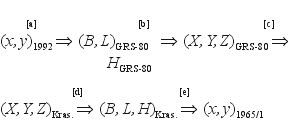 (1)
(symbole [a]-[e] oznaczają kolejne operacje elementarne w przekształceniu współrzędnych).
Tymczasem dla tego samego punktu w układzie 1965/1 istnieją już współrzędne archiwalne, pochodzące z dawnych wyrównań sieci na elipsoidzie Krasowskiego; oznaczmy je
(~x, ~y)1965/1 (rys. 1).
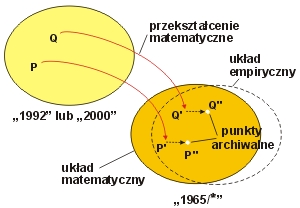
Rys.1. Współrzędne matematyczne a współrzędne empiryczne (archiwalne).
Na podstawie takiego lub podobnych testów przeprowadzonych w różnych strefach układu „1965” możemy się przekonać, że wyniki przekształceń matematycznych (1) nie pokryją się na ogół z wartościami odpowiadających współrzędnych archiwalnych, a różnice (maksymalne w strefie 3 dochodzą nawet do 1 m) mają wyraźne cechy lokalnych lub globalnych (strefowych) odchyleń systematycznych. Biorąc pod uwagę, że nowo pozyskane współrzędne punktów I klasy w układzie „1992” charakteryzują się względnie wysoką dokładnością (w świetle przeprowadzonej analizy, przeciętny błąd położenia punktu względem nawiązawczej sieci POLREF i EUREF-POL nie przekracza wartości 0,02 m, mimo że do nowego wyrównania użyto zbiorów obserwacji archiwalnych) można przypuszczać, że relatywnie niewielkie różnice pomiędzy współrzędnymi obliczonymi a archiwalnymi są wynikiem odmienności dawnych rozwiązań i opracowań numerycznych sieci, najpierw na elipsoidzie Krasowskiego, a następnie w poszczególnych strefach układu „1965” (należy mieć przy tym na uwadze nieporównywalne w różnych epokach możliwości techniki obliczeniowej).
Przyjmiemy umownie, że współrzędne przeliczone generują matematyczny układ „1965”, zaś współrzędne archiwalne - odpowiadający układ empiryczny „1965”. Zakładamy, że układ empiryczny wraz z całym archiwum map, poza doraźną aktualizacją (do roku 2009 – w świetle cytowanego rozporządzenia Rady Ministrów), nie powinien podlegać już zasadniczym modernizacjom. Dlatego wszelkie przeliczenia punktów z nowych układów odwzorowawczych elipsoidy GRS-80 (z systemu ETRF’89) do układu „1965” powinny zakładać „dopasowanie” współrzędnych obliczonych do istniejących już odpowiedników empirycznych (archiwalnych). Oznacza to konieczność zastosowania dodatkowego przekształcenia współrzędnych:
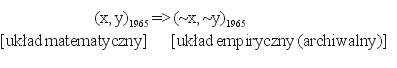 (2)
Istnieją różne „szkoły” wykonania tego zadania. Omówimy je pokrótce. Tymczasem zauważmy, że analogiczny problem wystąpi również przy przeliczaniu odwrotnym do (1), czyli z układu „1965” do układu „1992” lub „2000” i to – jak się wydaje – będzie stanowić istotne zadanie technologiczne w najbliższych latach. O ile operacja (2) oznacza pewne „świadome” zniekształcanie układu „dobrego”, operacja odwrotna będzie oznaczać „naprawianie” (korygowanie) zniekształconego układu archiwalnego (po to, by wejść do układu nowego z możliwie najlepszym efektem jakościowym).
W przykładowym przekształceniu (1), które według przyjętej umowny generuje układ matematyczny „1965”, występuje operacja [c], której geneza nie jest jednak „czysto” matematyczna. Jak już wspomniano we wcześniejszych wykładach, parametry owej transformacji [c] estymowano na podstawie punktów sieci POLREF (dysponowano współrzędnymi punktów tej sieci w obu układach elipsoidalnych). Warto w tym miejscu nadmienić, że uzyskane w tej estymacji odchyłki współrzędnych miały wartość przeciętną ok. 0,20 m. Pomimo takiego efektu stochastycznego przyjmujemy, że ostateczna formuła transformacyjna, definiująca niejako na nowo położenie elipsoidy Krasowskiego (obecnie względem elipsoidy GRS-80) ma charakter matematycznego (stałego) założenia. W związku z tym całkowita odchyłka pomiędzy matematycznym a empirycznym układem „1965”, kumuluje się na końcowym etapie przekształcenia współrzędnych i jako taka tylko jest przedmiotem oceny lub podejmowania decyzji w aspekcie skutków.
Wpasowanie w układ empiryczny
Jeśli różnice pomiędzy współrzędnymi obliczonymi (matematycznymi) a empirycznymi (archiwalnymi) na punktach łącznych nie przekraczają poziomu dopuszczalnego błędu współrzędnych, to mamy do czynienia z przypadkiem, kiedy korekta typu (2) nie jest konieczna. W typowych sytuacjach praktycznych takie „zdarzenie dokładnościowe” będzie raczej wyjątkiem. W ogólności zajdzie potrzeba jakiejś konkretnej realizacji formuły korekcyjnej typu (2). Wyróżnimy w związku z tym następujące rodzaje korekt:
- globalne (dla całej strefy) o charakterze przekształcenia wiernokątnego,
- globalne o charakterze afinicznym,
- lokalne (ograniczone do obszaru opracowania, fragmentu strefy) oparte na danym lokalnym zbiorze punktów dostosowania (punktów łącznych), realizowane przy zastosowaniu transformacji Helmerta oraz dodatkowej korekty (korekty posttransformacyjnej) Hausbrandta [14], mającej na celu „wyzerowanie” odchyłek na punktach łącznych i odpowiednie skorygowanie z tego tytułu wszystkich pozostałych punktów transformowanych.
Korekty globalne różnią się zasadniczo od korekt lokalnych tym, że nie wymagają odszukiwania, identyfikowania i kontroli poprawności lokalnego układu punktów łącznych. Funkcje realizujące korekty globalne można wyznaczyć jednokrotnie dla każdej strefy układu „1965” (na podstawie dostępnych w różnych układach współrzędnych punktów I klasy) i „wstawić” je na stałe do programu transformującego w formie odpowiedniej procedury. Rozwiązanie takie zastosowano w pakiecie programów GEONET_unitrans [10], gdzie mamy możliwość wyboru następujących opcji transformacji na wejściu do (lub wyjściu z) układu „1965”:
- matematycznej,
- matematycznej skorygowanej (z globalną korektą konforemną),
- empirycznej (z globalną korektą afiniczną).
Opcja korekt lokalnych, wymagająca dodatkowych informacji zewnętrznych (wykazu współrzędnych punktów łącznych) realizuje się natomiast za pomocą dodatkowego programu transformacji płaskiej.
Globalna korekta konforemna dla stref układu „1965” jest reprezentowana przez wielomian zmiennej zespolonej (stopnia 1 dla strefy 5 lub stopnia 5 dla wszystkich pozostałych stref układu „1965”). Opiera się ona na założeniu, że przekształcenie pomiędzy układem empirycznym a matematycznym (lub odwrotnie) zachowuje cechę wiernokątności. Lokalnie korekta ta nie zmienia kształtu transformowanej sieci, co ma znaczenie np. przy opracowywaniu sieci GPS. Na podstawie testów przeprowadzonych w poszczególnych strefach układu „1965” można stwierdzić, że globalne korekty konforemne powodują zmniejszenie odchyłek (względem układu empirycznego) przeciętnie o ok. 70% (por. tab. 2). Korekta może być stosowana dwukierunkowo, tzn. także przy przekształceniach odwrotnych (z układu „1965” do układu „1992” lub „2000”).
Globalna korekta afiniczna, realizowana za pomocą wielomianów stopnia 5-6, sprowadza układ matematyczny do postaci odchylającej się od układu empirycznego przeciętnie już tylko o rząd kilku centymetrów (od 0,02 do 0,05 m). Globalna korekta afiniczna może mieć zastosowanie zwłaszcza przy przekształcaniu wektorowych obrazów map. Korekta może być stosowana dwukierunkowo („do” i „z” układu „1965”). Ograniczeniem stosowalności globalnych korekt afinicznych jest granica danej strefy.
Korektę lokalną realizuje się dwuetapowo: najpierw za pomocą znanej transformacji Helmerta (liniowej transformacji konforemnej) na podstawie zidentyfikowanych punktów dostosowania klasy wyższej niż klasa punktów transformowanych, a następnie poprzez tzw. korektę Hausbrandta [14], mającą na celu „redystrybucję” powstałych odchyłek na wszystkie punkty transformowane (w szczególności punkty dostosowania zachowują dokładnie współrzędne archiwalne). W odniesieniu do osnów geodezyjnych korekta tego rodzaju proponowana jest m.in. w projektach nowych przepisów technicznych (Instrukcja G-2 [13] oraz Wytyczne Techniczne G-1.10 [6]). Pomimo bardzo klarownego geometrycznie podejścia, korekta lokalna – oprócz wspomnianych już wymagań dodatkowych w zakresie punktów łącznych – ma pewne wady technologiczne. Dotyczy to kwestii niejednoznaczności „na styku” dwóch niezależnie opracowywanych obiektów oraz problemu możliwej nieaktualności danych, na podstawie których wyznacza się lokalne parametry transformacji.
n Niejednoznaczność wynika wprost z pewnej dowolności lokalnego układu punktów dostosowania (punktów łącznych transformacji). Jeśli dwa niezależnie opracowywane obiekty (sieci) sąsiadują ze sobą i korzystają z różnych (ale niekoniecznie rozłącznych) zbiorów punktów dostosowania wówczas powstaje problem uzgodnienia współrzędnych punktów położonych na granicy dwóch obszarów („uzgodnienie styków”) – rys. 2. Opisany efekt nie musi być wynikiem jakiegoś błędnego punktu dostosowania. Jest to efekt geometryczny, który można zobrazować na przykład zastąpieniem powierzchni regularnej wycinkami płaszczyzn. W przeciwieństwie do omawianych korekt lokalnych korekty globalne prowadzą do wyników jednoznacznych, pod warunkiem, że są skonstruowane jako funkcje ciągłe dla całej strefy odwzorowawczej. Nie analizujemy już szerzej możliwych efektów „większego kalibru”, kiedy przy niekorzystnym układzie lub niewielkiej liczebności punktów dostosowania „zdarzą się” współrzędne z istotnym błędem. Jeśli weźmiemy pod uwagę bliskie już potrzeby przetwarzania dotychczasowego zasobu numeryczno-kartograficznego z układu „1965” do układu „2000”, to względy ekonomiczne (masowość przetwarzania) i niezawodnościowe (do czego nawiązano powyżej) oraz kwestie inne tu wymieniane uzasadniają przyjęcie automatycznych korekt globalnych, jako „generalnie” zweryfikowanego elementu przetwarzania. Dodajmy, że element ten jako część programu jest dla użytkownika „niewidzialny”.
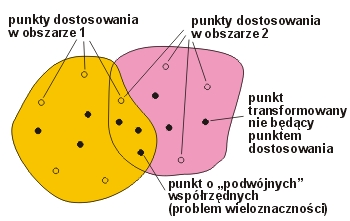
Rys. 2. Ilustracja do problemu niejednoznaczności korekt lokalnych
n Problem nieaktualności danych może zaistnieć w sytuacji, gdy współrzędne archiwalne dotyczą innych położeń znaków fizycznych niż ich stan obecny, tj. na moment wykonywania nowych pomiarów. Łatwo zauważyć, że korekta lokalna spowoduje przemieszczenie układu punktów transformowanych, a tym samym całą „treść” nowego pomiaru względem archiwalnego obrazu mapy. Tej wady nie mają korekty globalne (współczynniki korekt globalnych wyznacza się wprawdzie na podstawie nowo wyrównanych współrzędnych punktów I klasy na elipsoidzie GRS-80, ale to wyrównanie zrealizowano, jak wiadomo, opierając się na tych samych zbiorach obserwacyjnych, z których pozyskiwano współrzędne w układzie „1965”).
Pewną osobliwą różnicą pomiędzy korektami globalnymi i lokalnymi jest to, że korekty globalne można realizować dwukierunkowo pomiędzy matematycznym układem „1965” a jego odpowiednikiem empirycznym: (x, y)1965 <=> (~x, ~y)1965 , czyli także jako odwrócenie ogólnego przekształcenia (2). Odwrotna korekta lokalna wymaga natomiast, by najpierw przekształcić „błędne” współrzędne do układu nowego, a dopiero na płaszczyźnie tego układu dokonać stosownych dopasowań transformacyjnych na podstawie punktów dostosowania (rys. 3). Oczywiście, takie postępowanie nie jest wadą korekt lokalnych, zmienia tylko w pewnym sensie kolejność operacji elementarnych.
Rys. 3. Schemat korekt odwrotnych: a) globalna , b) lokalna
Technika korekt konforemnych
W przypadku korekt konforemnych przekształcenie z układu matematycznego do układu empirycznego (lub odwrotnie) dokonuje się przy wykorzystaniu ogólnych wielomianów zespolonych:
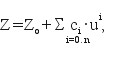 (3)
gdzie: argument zespolony u jest utworzony ze współrzędnych pierwotnych (w zależności od kierunku korekty będą to współrzędne matematyczne lub empiryczne):
u = ( ux, uy ) ; ux = (x - xo) · s , uy = (y - yo) · s,
x, y - współrzedne pierwotne, xo , yo - parametry centrujące,
s - parametr skalujący (normujący) dobrany tak, by w całym obszarze strefy
był spełniony warunek: | u | < 1,
ci = ( ai , bi) - zespolone współczynniki wielomianu wyznaczone jednokrotnie dla
całej strefy (wprowadzone na stałe do programu komputerowego),
Z = (X, Y) - współrzędne wynikowe (skorygowane, w układzie wtórnym),
Zo = (Xo, Yo) - pomocnicze współrzędne centrujące w układzie wtórnym.
W tabeli 1 [wejście na tabelę 1. tab_1] podano przykładowe parametry korekty konforemnej dla strefy 4. układu „1965”oraz fragment programu realizującego formułę wielomianu zespolonego. Ze względu na ograniczone ramy wykładu, nie rozwijamy już tematyki korekt afinicznych, które opierają się na ogólnych formułach wielomianowych. Komplet parametrów i funkcji korekcyjnych zarówno konforemnych, jak i afinicznych, dla wszystkich stref układu „1965” jest zaaplikowany w pakiecie GEONET_unitrans [10].
Ilustracją efektu zastosowania korekt globalnych niech będzie poniższy przykład. Wybrano 4 punkty I klasy położone w skrajnych miejscach strefy 4, układu „1965” (rys. 4). Wychodząc od współrzędnych geodezyjnych B,L tych punktów na elipsoidzie GRS-80, dokonano ich przekształcenia do układu „1965”, stosując opcję matematyczną, matematyczną skorygowaną (przy zastosowaniu korekty konforemnej według tabeli 1) oraz opcję empiryczną (z ogólną korektą wielomianową – bez warunku konforemności).
Rys.4 Układ punktów testowych w strefie 4. układu „1965”
Wyniki każdego przekształcenia porównano ze współrzędnymi katalogowymi (archiwalnymi) punktów w układzie „1965”. Rezultaty porównań prezentuje tabela 2.
Tab. 2. Ilustracja zmniejszania się odchyłek przy zastosowaniu korekt globalnych.
Statystyka odchyleń pomiędzy matematycznym a empirycznym układem „1965”
Tabela 3 podaje przeciętne (co do wartości bezwzględnej) i maksymalne odchylenia współrzędnych matematycznych (bez korekty i z korektami globalnymi) od współrzędnych archiwalnych, zidentyfikowane na punktach I klasy. Ze szczegółowej analizy różnic współrzędnych można wynieść, że istotne odchylenia „od matematyki” widoczne są zwłaszcza w strefie 3. układu „1965”, gdzie historycznie rzecz biorąc osnowa geodezyjna nie stanowiła jednolitego i jednorodnego układu obserwacyjnego. Drugie nie mniej istotne spostrzeżenie dotyczy strefy 5., gdzie zaznacza się widoczne przesunięcie układu empirycznego po osi X w granicach ok. 0,5 m.
Tab. 3. Statystyka odchyłek empirycznego układu „1965”
Narzędzia korekt lokalnych Na zakończenie niniejszego wykładu podamy jeszcze syntetyczne wzory dotyczące realizacji korekt lokalnych.
Transformacja Helmetra (przez podobieństwo lub liniowa transformacja konforemna). W pierwszym etapie wyznaczamy współczynniki transformacji na podstawie współrzędnych punktów dostosowania (łącznych). Oznaczmy {(xi , yi ): i = 1, 2, ... , n }, { (Xi , Yi ): i =1, 2, ... , n } dane zbiory współrzędnych tych punktów w odpowiednich układach: pierwotnym i aktualnym. Obliczamy najpierw współrzędne środków ciężkości zbiorów punktów w obu układach i dokonujemy odpowiedniego centrowania współrzędnych:
 (4)
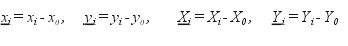 (5)
(dla wszystkich i = 1,2, ... , n) .
Szukane współczynniki transformacji wyrażają się wzorami:
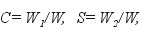 (6)
gdzie:
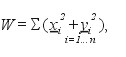 (7)
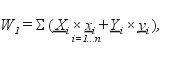 (8)
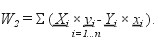 (9)
Teraz możemy już realizować samą transformację (przekształcenie współrzędnych z układu pierwotnego do wtórnego), stosując wzory:
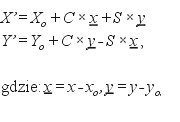 (10)
x, y - współrzędne punktu w układzie pierwotnym, X’, Y’ - współrzędne punktu po transformacji (w układzie wtórnym).
Dla wszystkich punktów dostosowania obliczamy stosowne odchyłki współrzędnych katalogowych (poprawki do współrzędnych z transformacji):
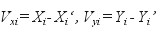 (11)
(i - wskaźnik punktu dostosowania), a na ich popdstawie - błąd transformacji jako średniokwadratową odchyłkę wypadkową punktu
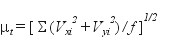 (12)
przy czym przyjmujemy f = n (zamiast f = n -2 ) uznając, że parametr mt jest tylko umowną miarą jakości dopasowania (w ujęciu stochastycznym parametr ten byłby wprawdzie pewnym oszacowaniem błędu położenia punktu, ale ocena taka nie jest dostatecznie wiarygodna, gdyż opisane zadanie zakłada uproszczony model stochastyczny dla wielkości, które nie są bezpośrednimi obserwacjami, a ponadto nadwymiarowość układu będzie w praktyce na ogół istotnie ograniczona). Niezależnie od powyższych wątpliwości, odchyłki i błąd transformacji są podstawą do jakiejś oceny poprawności współrzędnych punktów dostosowania w danej klasie sieci. Współczynniki transformacji C, S mają następującą interpretację:
 (13)
Korekta posttransformacyjna Hausbrandta. W wyniku zastosowania wzorów (10) wszystkie punkty dostosowania otrzymają nowe współrzędne, które nie muszą się pokrywać z istniejącymi już współrzędnymi katalogowymi (archiwalnymi) tych punktów. Różnice określone wzorami (11) są odchyłkami transformacji. Aby nie zmieniać dotychczasowych współrzędnych (archiwalnych) stosujemy pewnego rodzaju dodatkowe „uzgodnienie” współrzędnych, które nazywa się korektą Hausbrandta [14]. Polega ona na tym, że współrzędne punktów dostosowania w układzie wtórnym pozostawia się bez zmiany (można powiedzieć inaczej, że do współrzędnych transformowanych (10) dodaje się wartości poprawek (11), powracając tym samym do wartości współrzędnych katalogowych), natomiast wszystkim pozostałym punktom transformowanym (poza punktami dostosowania) przydziela się poprawki wyznaczone przy zastosowaniu specjalnych wzorów interpolacyjnych (w ten sposób następuje niejako świadome deformowanie wyników transformacji Helmerta, narzucone przez warunek niezmienności współrzędnych katalogowych):
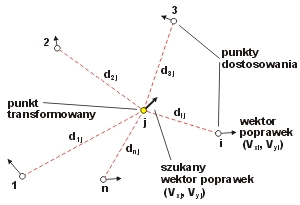
Rys. 5. Ilustracja do zadania korekty Hausbrandta
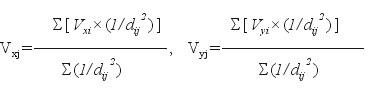 (14)
(sumowania po i = 1, 2, ... , n ; j -wskaźnik punktu transformowanego)
Jak widać, przedstawione wzory wykazują podobieństwo do średnich ważonych, gdzie wagi są odwrotnościami kwadratów odległości danego punktu o wskaźniku j (w zbiorze wszystkich punktów transformowanych) od punktu dostosowania o wskaźniku i (w zbiorze punktów dostosowania). Ilustruje to rys. 4. Długości dij obliczamy na podstawie współrzędnych pierwotnych. Wielkości poprawek (14) dodajemy do współrzędnych po transformacji, czyli do współrzędnych wyznaczonych przy pomocy wzorów (10).
Na koniec podamy pewną interpretację fizyczną korekty Hausbrandta dla przypadku wpasowywania się w istniejące współrzędne archiwalne lub w przekształceniu odwrotnym. Wyobraźmy sobie, że płaski układ, który określamy jako empiryczny jest „sztywny”, natomiast układ matematyczny - „elastyczny”. Poprzez lokalne rozciągania i kurczenia układu elastycznego (przy zachowaniu jego płaskości) doprowadzamy do wzajemnego pokrycia się punktów łącznych obu układów. W efekcie wszystkie punkty układu elastycznego otrzymują przesunięcia mierzone wielkościami (14). Analogiczna interpretacja będzie dotyczyć przekształcenia odwrotnego (wówczas sztywnym będzie na przykład układ „1992” lub „2000”, zaś elastycznym - odpowiednie przekształcenie empirycznego układu „1965”).
Roman Kadaj jest profesorem nauk technicznych, kierownikiem Katedry Geodezji na Akademii Rolniczej w Krakowie
Literatura:
[1] Projekt rozporządzenia Rady Ministrów w sprawie państwowego systemu odniesień przestrzennych, wersja 2000-01-15, GUGiK 1999;
[2] Ekspertyza dotycząca odwzorowania kartograficznego dla wielkoskalowych opracowań geodezyjnych i kartograficznych w Polsce, opracowanie wykonane przez zespół pod przewodnictwem prof. dr. hab. Włodzimierza Barana, Polska Akademia Nauk, Komitet Geodezji, Sekcja Sieci Geodezyjnych;
[3] Państwowy układ współrzędnych 1992, opracowanie wykonane przez dr. Henryka Balcerzaka (mat. do użytku służbowego), Główny Geodeta Kraju, Warszawa 1995;
[4] Balcerzak J., Odwzorowanie Gaussa-Krügera w szerokiej 12° strefie dla obszaru Polski, IX Szkoła Kartograficzna, Komorowo, 10-14 października 1994;
[5] Gajderowicz I., Kartografia matematyczna dla geodetów, ART Olsztyn 1991, nowa edycja 1999;
[6] Kadaj R., Formuły odwzorowawcze i parametry układów współrzędnych, Wytyczne Techniczne G-1.10 (projekt), wykonano na zlecenie GUGiK, Warszawa, grudzień 1999;
[7] Kadaj R., Procedury transformacji pomiędzy państwowymi układami współrzędnych. Opis procedur bazy GEOS w CODGiK, GEOMAT Sp. z o.o. w Poznaniu, wrzesień 1999;
[8] Kadaj R., Układ Kartograficzny PUK 2000, (projekt wdrożeniowy), INFOPRO S.A. Przedsiębiorstwo Projektowo-Wdrożeniowe, Warszawa, sierpień 1999;
[9] Panasiuk J., Balcerzak J., Gdowski B., The Roussilhe projection of the entire ellipsoid, 16th International Cartographic Conference, Cologne 1993, 1278-1286;
[10] GEONET_unitrans: uniwersalny program transformacji współrzędnych pomiędzy różnymi układami w obszarze Polski oraz programy pomocnicze. Opis pakietu. I wyd. 1977, nowa edycja 2000, ALGORES-SOFT s.c. Rzeszów.
[11] Krüger L.: Konforme Abbildung des Erdellipsoids in der Ebene. Pr. Geod. Instit. Neue Folge 51, Podstam 1912;
[12] Plewako M.: Enlargement of efficient application of L. Krüger’s algorithm for computation of rectangular coordinates in the Gauss- Krüger projection in a wide meridional zone. Zesz. Nauk. AGH, s. Geodezja, z.112, Kraków 1991, 105-117.
[13] Instrukcja Techniczna G-2 (projekt w wersji 2000), GUGiK.
[14] Hausbrandt S.: Rachunek wyrównawczy i obliczenia geodezyjne. T. II, PPWK Warszawa 1971
Opracowanie zamieszczono na Geoforum w styczniu 2006 r.
| 