|
Roman Kadaj
Przy tworzeniu map numerycznych bardzo często pojawia się potrzeba przeliczeń (transformacji) współrzędnych pomiędzy różnymi, dawnymi i nowymi, układami dla obszaru Polski. Jest to aktualnie jeden z istotnych problemów polskiej geodezji, zwłaszcza że obowiązuje w Polsce europejski system odniesień przestrzennych ETRS z nowo wprowadzonymi układami odwzorowawczymi.
Czyżby prawa i powinności geodety w rzeczy samej?
Dokonując pewnego rozrachunku z przeszłością, można by powiedzieć, że jednym z podstawowych praw geodety jest prawo do wiedzy na temat układów współrzędnych, w których realizuje istotę swojego dzieła. Negowanie lub ograniczanie tego prawa marginalizuje zawód geodety, wpływa także na jakość jego dzieł, składających się przecież na pewien zasób dóbr powszechnych. Przychodzą mi tu na myśl epizody związane z przeliczaniem współrzędnych punktów pomiędzy strefami układu „1965”, kiedy z powodu trudności w dostępie do odpowiednich danych podstawowych stosowano różne „narzędzia” empiryczne, nie bez szkody dla jakości produktów finalnych. Można mieć nadzieję, że podobne przykłady należą już raczej do przeszłości i kształcenie w zakresie podstaw geodezji i kartografii będzie mieć także wymierny sens praktyczny. Należy podkreślić, że wiedza z zakresu powszechnie stosowanych układów współrzędnych ma charakter uniwersalny, a posiadanie jej jest nie tylko prawem, lecz także powinnością każdego geodety.
Odwzorowanie Gaussa-Krügera wiecznie żywe
Różne państwowe układy współrzędnych można sklasyfikować przede wszystkim pod względem ich teoretycznej genezy, tj. przyjętej matematycznej powierzchni odniesienia (elipsoidy) generalizującej lokalnie lub globalnie kształt geoidy oraz rodzaju i zasięgu obszarowego zastosowanego odwzorowania. Ta ostatnia kwestia była w minionych latach przedmiotem wielu dyskusji, a dotyczyła wyboru konkretnych odwzorowań dla map wielkoskalowych i topograficznych. Jednym z kryteriów wyboru była wielkość maksymalnych zniekształceń liniowych, istotna zwłaszcza w zakresie map wielkoskalowych (mapy zasadniczej). Kompromis w tym względzie doprowadził formalnie do utrzymania jednostrefowego odwzorowania Gaussa-Krügera dla opracowań kartograficznych w skalach mniejszych od 1:5000 oraz na przyjęciu 4-strefowego odwzorowania Gaussa-Krügera dla mapy zasadniczej (stanowiło to w istocie powrót do koncepcji dawnego układu „1942”) [1, 2]*.
Na elipsoidzie Krasowskiego
W Polsce, podobnie jak w innych państwach byłego Układu Warszawskiego, obowiązywała od roku 1952 elipsoida Krasowskiego z punktem przyłożenia do geoidy w Pułkowie i lokalną orientacją azymutalną. Był to system przyjęty w b. ZSRR w roku 1942, stąd też nazywany Pułkowo ’42. Elipsoida Krasowskiego zastąpiła w Polsce dawną elipsoidę Bessela z punktem przyłożenia do geoidy w Borowej Górze. W wyniku wzajemnego powiązania państwowych sieci astronomiczno-geodezyjnych elipsoida Krasowskiego (w systemie Pułkowo ’42) stała się bazą odniesienia dla polskich osnów geodezyjnych i układów odwzorowawczych.
„1942”
Do połowy lat 60. obowiązywał w Polsce układ współrzędnych zwany „1942” (od daty wprowadzenia systemu elipsoidalnego). Układ ten powstał w wyniku zastosowania odwzorowania Gaussa-Krügera na elipsoidzie Krasowskiego, przy czym obejmował dwa podsystemy (rys. 1):
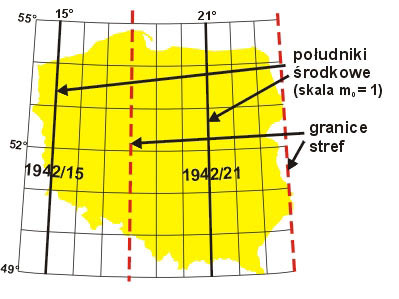
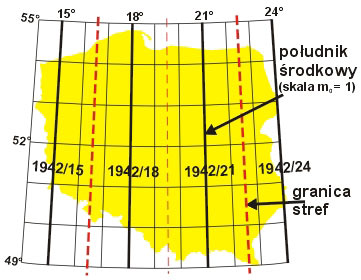
Rys. 1. Układ „1942” a) odwzorowanie pasów 6-stopniowych, b) odwzorowanie pasów 3-stopniowych
- odwzorowanie w pasach południkowych o szerokości 6°. W wyniku tego na obszarze Polski powstały dwie strefy odwzorowawcze: z południkami środkowymi 15° i 21°; nazywamy je pomocniczo: 1942/15 (6) i 1942/21 (6). Odwzorowanie to miało zastosowanie dla map średnio- i małoskalowych (skale mniejsze od 1:5000). Zniekształcenia odwzorowawcze zmieniały się od 0 (na południku środkowym każdej strefy) do ok. + 59 cm/km (na brzegach strefy)
- odwzorowanie w pasach południkowych o szerokości 3°. W wyniku tego na obszarze Polski powstały cztery strefy odwzorowawcze: z południkami środkowymi 15°, 18°, 21°, 24°; oznaczamy je pomocniczo: 1942/15 (3), 1942/18 (3), 1942/21 (3), 1942/24 (3). Odwzorowanie to miało zastosowanie dla map wielkoskalowych (skala 1:5000 i większe). Zniekształcenia odwzorowawcze na brzegach stref dochodziły do +15 cm/km.
„1965” i GUGiK-80
Od końca lat 60. w służbie cywilnej zaczęto wprowadzać nowy, 5-strefowy układ odwzorowawczy (oparty na tym samym systemie elipsoidalnym) zwany krótko układem „1965”. Kraj został podzielony na pięć stref (rys. 2),
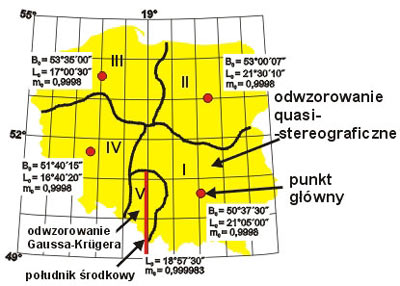
Rys. 2. Podział układu „1965” na strefy
przy czym w strefach 1, 2, 3, 4 zastosowano tzw. odwzorowanie quasi-stereograficzne (Roussilhe projection) (zob. np. [5], [9]), natomiast w strefie 5 – zmodyfikowane odwzorowanie Gaussa-Krügera. Każde odwzorowanie quasi-stereograficzne jako wiernokątne odwzorowanie płaszczyznowe elipsoidy definiuje się, określając położenie punktu głównego (punktu styczności płaszczyzny z powierzchnią elipsoidy) oraz skalę odwzorowania w tym punkcie, będącą równocześnie skalą podobieństwa odwzorowania. W strefach 1-4 układu „1965” przyjęto skalę w punkcie głównym m0 = 0,9998, tzn. zniekształcenie odwzorowawcze w tym punkcie wynosiło z założenia – 20 cm/km. Układ „1965” był przeznaczony głównie do tworzenia i eksploatacji mapy zasadniczej.
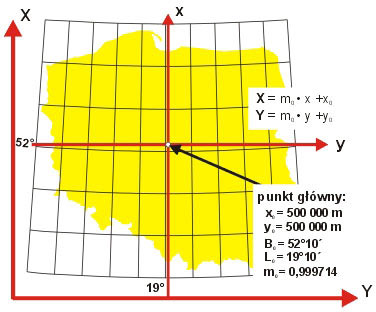
Rys. 3. Układ „GUGiK-80”, odwzorowanie quasi-stereograficzne
Dla map przeglądowych w skalach 1:100 000 i mniejszych przyjęto natomiast układ oparty na jednostrefowym odwzorowaniu quasi-stereograficznym obszaru Polski nazwany GUGiK-80 (rys. 3). Punkt główny odwzorowania wybrano w przybliżeniu w środku Polski (B0 = 52°10´, L0 = 19°10´).
Na elipsoidzie WGS-84 (GRS-80)
Od początku lat 90. podjęto prace mające na celu włączenie obszaru Polski do europejskiego systemu odniesień przestrzennych ETRS (European Terrestrial Reference System), będącego częścią światowego systemu ITRS, a reprezentowanego przez układ 35 stacji bazowych, zwany w skrócie ETRF lub EUREF (European Terrestrial Reference Frame). Na obszarze Polski utworzono najpierw sieć EUREF-POL złożoną z 11 punktów bazowych, którą następnie zagęszczono siecią ok. 350 punktów, zwaną w skrócie POLREF. Wszystkie pomiary wykonane zostały techniką GPS (Global Positioning System). Sieci EUREF-POL i POLREF stały się z kolei podstawą ponownego wyrównania dawnej sieci astronomiczno-geodezyjnej i triangulacji wypełniającej (sieci I klasy), a następnie także sieci poziomej II klasy. Wszystkie obliczenia wykonano już na nowej elipsoidzie systemu EUREF zwanej w skrócie GRS-80. Nazwa pełna „Geodetic Reference System 1980” dotyczy w istocie szerszego zbioru parametrów geometryczno-fizycznych opisujących Ziemię. W latach późniejszych wprowadzono zmodyfikowany zbiór parametrów znany pod nazwą WGS-84 (World Geodetic System 1984), który praktycznie nie zmieniał geometrii elipsoidy. Dlatego zamiast nazwy elipsoida (lub układ elipsoidalny) GRS-80 notujemy też równoważnie: WGS-84.
„1992” i „2000”
Zarówno dla osnów poziomych, jak i opracowań kartograficznych przyjęto dwa nowe systemy odwzorowawcze elipsoidy GRS-80 [1-4]:
- jednostrefowe dla obszaru Polski odwzorowanie Gaussa-Krügera z południkiem środkowym L0 = 19° i skalą podobieństwa m0 = 0,9993 (ostatnie założenie ma na celu równomierny rozkład zniekształceń liniowych, od –70 cm/km na południku środkowym do ok. +90 cm/km w skrajnych, wschodnich obszarach Polski) – rys. 4, 5. Układ został nazwany skrótowo „1992”. Obecnie stanowi podstawę do wykonywania nowych map w skalach 1:10 000 i mniejszych. Ze względu na znaczne zniekształcenia liniowe układ nie jest rekomendowany do wielkoskalowych opracowań kartograficznych;
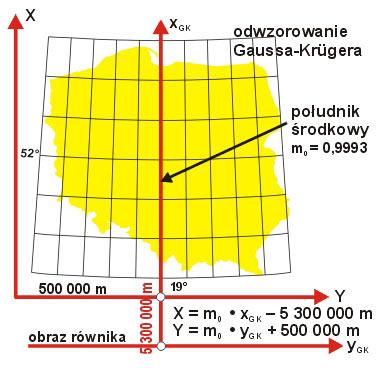
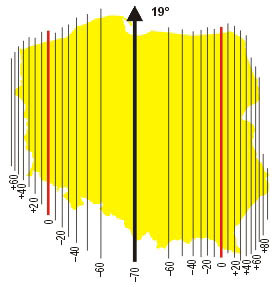
Rys. 4, 5. Układ „1992” oraz izolinie zniekształceń elementarnych [cm/km] w układzie „1992”
- czterostrefowe odwzorowanie Gaussa-Krügera elipsoidy GRS-80 w pasach 3-stopniowych, zwane skrótowo układem „2000”. W tym przypadku koncepcja nawiązuje do dawnego układu „1942”. Różnica polega jednak na odmienności przyjętych elipsoid odniesienia oraz na zastosowaniu dodatkowej skali podobieństwa (skali kurczenia na południku środkowym). W układzie „2000” zastosowano skalę m0 = 0,999923, która realizuje kompromis w rozłożeniu zniekształceń liniowych (od –7,7 cm/km na południku środkowym strefy do maksymalnie ok. +7 cm/km na brzegu strefy).
Inne układy
Oprócz wymienionych już układów współrzędnych pełna problematyka transformacyjna nie może pomijać także innych układów, z którymi możemy mieć do czynienia przy kompilacji danych z różnych źródeł. Wymienimy tu przede wszystkim:
- uniwersalne poprzeczne odwzorowanie Mercatora UTM (Universal Transverse Mercator Projection) stosowane na świecie do celów nawigacyjnych i wojskowych. Jest to odwzorowanie Gaussa-Krügera w pasach 6-stopniowych, ze skalą na południku środkowym m0 = 0,9996 (zniekształcenie na tym południku wynosi –40 cm/km). W tym miejscu należy się słowo komentarza dotyczące nazewnictwa. Otóż przyjmuje się w zasadzie, że oryginalne odwzorowanie Gaussa-Krügera (wiernokątne walcowe poprzeczne odwzorowanie elipsoidy) nie zmienia skali południka środkowego (m0 = 1). W przypadku przeciwnym używamy też nazwy „modyfikowane odwzorowanie...”. W krajach anglosaskich przyjmuje się zaś nazwę „poprzeczne odwzorowanie Mercatora”. Odwzorowanie UTM zostało wprowadzone pierwotnie na elipsoidzie Hayforda, obecnie zaś zarówno w zastosowaniach cywilnych, jak i wojskowych obowiązuje elipsoida GRS-80 (WGS-84);
- układy lokalne miast powstałe obok układu „1965” poprzez przyjęcie płaszczyzny odniesienia przybliżającej lokalny przebieg geoidy lub adaptację dawnych układów katastralnych. W zasadzie definicje układów lokalnych nie przewidują wprowadzenia ani redukcji odwzorowawczych obserwacji ani redukcji na poziom odniesienia (zakłada się, że płaszczyzna odniesienia jest położona na średnim poziomie topograficznym obszaru). Pociąga to za sobą pewne błędy systematyczne, które mogą być zaniedbywalne tylko przy pewnej ograniczonej rozciągłości obszarowej układu.
Zwyciężyła tradycja europejska
Ograniczając się do powyższej listy najważniejszych praktycznie układów, należy stwierdzić, że za wyjątkiem „1965” (w strefach 1-4) oraz GUGiK-80 wszystkie pozostałe układy, wywodzące się z elipsoidy GRS-80 lub Krasowskiego, powstały jako aplikacje odwzorowania Gaussa-Krügera. Procedura realizacji tego odwzorowania stanowić będzie zatem istotny element procesu przeliczeń współrzędnych pomiędzy różnymi układami. Przyjęcie odwzorowania Gaussa-Krügera jako podstawy nowych definicji państwowych układów współrzędnych, np. jednolitego układu „1992”, ma swoją genezę w tradycji europejskiej (zwłaszcza niemieckiej).
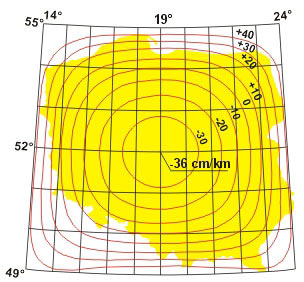
Rys. 6. Izolinie zniekształceń elementarnych [cm/km] w układzie PUK 2000 (odwzorowanie analityczne wiernokątne), © INFOPRO S.A. w Warszawie
Nie znaczy to jednak, że odwzorowanie to jest pod względem wielkości maksymalnych zniekształceń liniowych najkorzystniejsze dla Polski (z uwagi na bardziej kołowy niż wydłużony kształt kraju). Lepsze efekty (zniekształcenia liniowe mniejsze o ok. 50% w stosunku do układu „1992”) można uzyskać, korzystając z innych rodzajów odwzorowań konforemnych. Przykładem może być jednolite dla obszaru Polski odwzorowanie wiernokątne, nazwane umownie PUK 2000 (rys. 6), skonstruowane specjalnie dla map branżowych [9].
Transformacje pomiędzy układami różnych elipsoid odniesienia
Przeliczenie współrzędnych pomiędzy układami płaskimi wywodzącymi się z różnych elipsoid odniesienia, np. pomiędzy układem „1965” a układem „1992”, powinno się w zasadzie odbywać poprzez pośrednie przejście (transformację) pomiędzy układami współrzędnych geograficznych geodezyjnych (krótko: geodezyjnych) B, L, H (szerokość, długość i wysokość elipsoidalna – rys. 7)
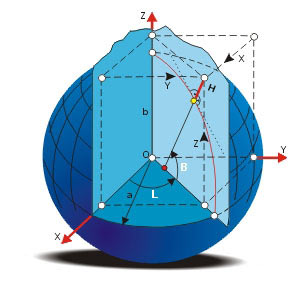
Rys. 7. Współrzędne geodezyjne i kartezjańskie centryczne
lub współrzędnych kartezjańskich centrycznych X, Y, Z (względnie „geocentrycznych”, jeśli środek elipsoidy pokrywa się ze środkiem mas Ziemi, jak zakłada się dla elipsoidy GRS-80) obu elipsoid. Symbolicznie pokazuje to rysunek 8.
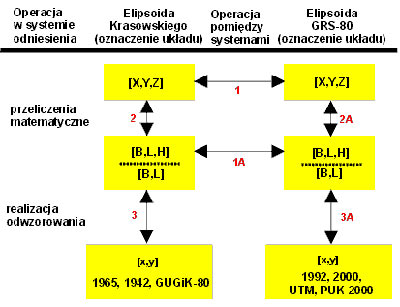
Rys. 8. Przejścia pomiędzy układami odwzorowawczymi elipsoid za pośrednictwem układów elipsoidalnych. Dwukierunkowe strzałki wskazują, że przeliczanie współrzędnych może przebiegać w obu kierunkach, przy czym jedno (umowne) zwane jest transformacją „wprost”, zaś przeciwne
– „odwrotną”; przeliczenia 1 i 1a mają znaczenie alternatywne.
Rysunek 9 ilustruje z kolei wzajemne położenie układów kartezjańskich elipsoid. Elipsoidy Krasowskiego i GRS-80 nie są ściśle koncentryczne i równoległoosiowe. Pomiędzy układami obu elipsoid zachodzą związki transformacji przestrzennej przyjmowanej jako transformacja przez podobieństwo (7-parametrowa).
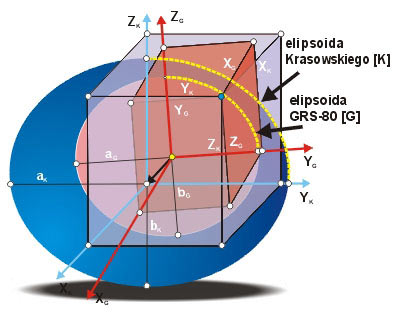
Rys. 9. Ilustracja wzajemnego położenia elipsoid. Przeciętny odstęp elipsoid w obszarze Polski ok. 35 m
Parametry tej transformacji (3 – przesunięcia, 3 – obroty osiowe oraz 1 – zmiany skali) wyznaczono (estymowano) w GUGiK na podstawie punktów sieci POLREF. Aby takie wyznaczenie mogło mieć miejsce, punkty te musiały posiadać współrzędne wyznaczone w obu układach elipsoidalnych.
Każda z ukazanych na rysunku 8 operacji przejścia z jednego układu do drugiego odbywa się za pośrednictwem ściśle określonych funkcji transformacyjnych (odwzorowawczych) i ich parametrów liczbowych. Podamy je w kolejnych wykładach, ograniczając się na razie do przedstawienia zasad ogólnych.
Powstaje praktyczne pytanie, czy można bezpośrednio przeliczyć współrzędne płaskie, na przykład z układu „1965” do układu „1992”, poprzez zastosowanie odpowiednich przekształceń dwuwymiarowych. Wbrew temu, co sugeruje się niekiedy w praktyce, przeliczenie takie nie jest formalnie poprawne bez udziału przynajmniej przybliżonej informacji o wysokości elipsoidalnej punktu w systemie, z którego wychodzimy (jak wskazuje rys. 8, aby przejść pomiędzy systemami, należy do współrzędnych B, L dołączyć wysokość elipsoidalną H).
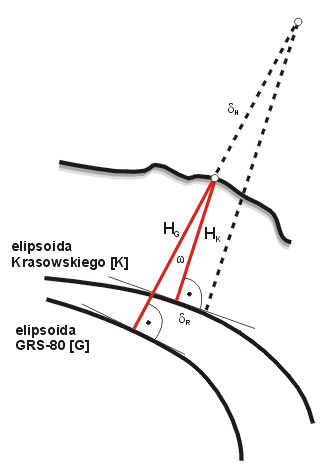
Rys. 10. Wpływ wysokości na poziome położenie punktu
Rysunek 10 pokazuje w związku z tym, jak zmiana wysokości punktu wpływa na zmianę jego położenia poziomego przy przejściu z jednej elipsoidy na drugą. Załóżmy, że wysokość została określona z pewnym błędem dH i oszacujmy, jak wielce błąd ten wpływa na transformowane współrzędne płaskie. Z informacji o wzajemnym położeniu elipsoid wynika, że maksymalna kątowa rozwartość normalnych (poprowadzonych z tego samego punktu na powierzchni Ziemi do obu elipsoid) ma wartość rzędu 7˝. Łatwo wyliczamy, że wpływ błędu wysokości na przesunięcie „poziome” punktu wynosi:
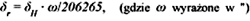
tj. ok. 0,34 mm na każde 10 m błędu wysokości. Dla wielu zadań geodezyjnych, z wyjątkiem problematyki osnów wyższych klas (np. w zadaniach przekształceń kartograficznych), wielkość ta może być rzeczywiście zaniedbywalna, nawet gdy się założy, że punkt transformowany leży wprost na elipsoidzie (H = 0). Przy takim założeniu można rozważać ewentualnie bezpośrednie przejścia transformacyjne (wielomianowe) pomiędzy układami odwzorowawczymi różnych elipsoid, jakkolwiek musimy mieć świadomość popełniania pewnego błędu systematycznego.
Transformacje pomiędzy układami tej samej elipsoidy odniesienia
Problematyka powyższa wiąże się również z przeliczeniem współrzędnych pomiędzy różnymi strefami tego samego układu albo pomiędzy różnymi układami tej samej elipsoidy. Uniwersalną metodą postępowania jest pośrednie przejście na współrzędne geodezyjne danej elipsoidy, co ilustruje rysunek 11. Drugi sposób polega na zastosowaniu bezpośrednich przejść pomiędzy strefami lub układami wywodzącymi się z tej samej elipsoidy. W tym celu wykorzystujemy własność wiernokątności wszystkich interesujących nas odwzorowań, konstruując odpowiednie wielomiany za pomocą analitycznej funkcji zmiennej zespolonej.
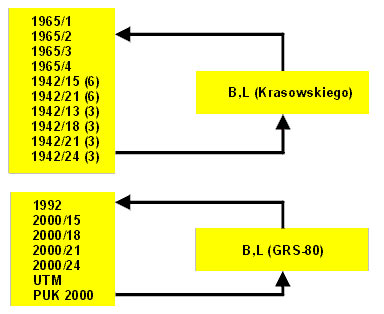
Rys. 11. Przykładowa ilustracja przejścia pomiędzy układami odwzorowawczymi tej samej elipsoidy odniesienia (strefy traktujemy jako odrębne układy): a) dla elipsoidy Krasowskiego , b) dla elipsoidy GRS-80
Z konkretnymi formułami transformacji współrzędnych, które mogą nas najbardziej interesować w praktyce kartografii numerycznej (mniemam, że zarysowuje się już w sposób naturalny taki dział kartografii), zapoznamy się w następnym, październikowym wykładzie. Należy dodać, że sama problematyka przeliczeń współrzędnych staje się kompletna dopiero przy równoległym „informowaniu” o elementach lokalnego pola zniekształceń odwzorowawczych. Są to: elementarna skala liniowa (ewentualnie przeliczona na elementarne zniekształcenie liniowe) oraz lokalna zbieżność południków zwana inaczej konwergencją. Wielkości te są potrzebne m.in. do redukowania obserwacji geodezyjnych.
Mam nadzieję przekonać Czytelnika, że problematyka transformacji współrzędnych nie jest wcale tak skomplikowana jak się ją niekiedy przedstawia w pracach teoretycznych, że są to zadania równie proste, jak wiele elementarnych zadań, z którymi mamy do czynienia w codziennej praktyce.
Roman Kadaj jest profesorem nauk technicznych, kierował Katedrą Geodezji na Akademii Rolniczej w Krakowie
Opracowanie 2006
* Spis literatury znajduje się w części ostatniej pt. „Osnowy a układy”.
| 